Question

Consider a water tank shown in the figure. It has one wall at x = L and can be taken to be very wide in the z direction. When filled with a liquid of surface tension S and density $\rho$, the liquid surface makes angle $\theta_0 (\theta_0 << 1)$ with the x-axis at x = L. If y(x) is the height of the surface then the equation for y(x) is:

(take $\theta(x) = \sin \theta(x) = \tan \theta(x) = \frac{dy}{dx}$, g is the acceleration due to gravity)

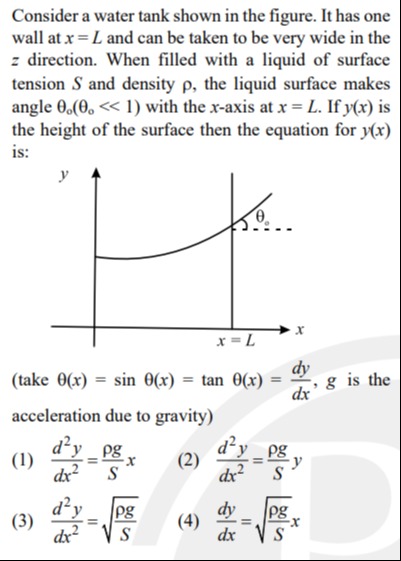
• A. $\frac{d^2y}{dx^2} = \frac{\rho g}{S}x$
• B. $\frac{d^2y}{dx^2} = \frac{\rho g}{S}y$
• C. $\frac{d^2y}{dx^2} = \sqrt{\frac{\rho g}{S}}$
• D. $\frac{dy}{dx} = \sqrt{\frac{\rho g}{S}}x$

Answer 1

Answer: (B)

$\frac{d^2y}{dx^2} = \frac{\rho g}{S}y$

Answer 2

The shape of the liquid surface is determined by the balance of forces due to surface tension and gravity. By considering the pressure difference across the curved liquid surface and using the small angle approximation, the equation for y(x) can be derived.