Question

Consider a very long stick of length $2{\text{R}}$ which extends from just above the surface of the earth to a radius ${\text{3R}}$ . If initial conditions have been set up so that this stick moves in a circular orbit while always pointing radially, find the period of the orbit. ( $g$ represents the acceleration due to gravity on the surface of the earth).

A) $6\pi \sqrt {\dfrac{R}{{2g}}}$
B) $2\pi \sqrt 6 \sqrt {\dfrac{R}{g}}$
C) $\pi \sqrt 6 \sqrt {\dfrac{R}{g}}$
D) None of these

Answer 1

Hint:. To obtain the expression for the period of the orbit of the stick, we have to obtain the angular velocity of its rotation. For this, we have to find the gravitational force and centripetal force acting on the stick as it rotates. Considering a small element of some thickness of the stick will help us in our computations. The centre of mass of the stick will be at its midpoint.

Formulas used:
-The gravitational force acting on a body at the surface of the earth is given by, ${F_g} = \dfrac{{GMm}}{{{r^2}}}$ where $G$ is the gravitational constant, $M$ is the mass of the earth, $m$ is the mass of the body and $r$ is the distance from the centre of the earth to the surface.
-The centripetal force acting on a rotating body is given by, ${F_c} = mr{\omega ^2}$ where $m$ is the mass of the body, $r$ is the radius of the orbit and $\omega$ is the angular velocity of the body.
-The period of revolution of a body is given by, $T = \dfrac{{2\pi }}{\omega }$ where $\omega$ is the angular velocity of the body.

Complete step by step answer.
Step 1: Sketch the figure where a small element of the stick is considered.

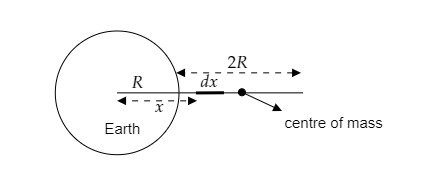
As seen in the above figure we consider a small element of thickness ${\text{dx}}$ and mass ${\text{dm}}$ at a distance of $x$ from the centre of the earth.
Then the linear mass density of that element will be $\lambda = \dfrac{{dm}}{{dx}}$
$\Rightarrow dm = \lambda dx$
The length of the stick is $l = 2R$ and the radius of the earth is $R$.
Let $M$ be the mass of the earth.
Step 2: Express the gravitational force acting on the small element to integrate it and obtain the gravitational force on the entire stick.
The gravitational force acting on the small element can be expressed as
$d{F_g} = \dfrac{{GMdm}}{{{x^2}}} = \dfrac{{GM\lambda dx}}{{{x^2}}}$ ------------ (1)
Now integrating equation (1) will give us the gravitational force acting on the entire stick.
i.e., ${F_g} = \int\limits_R^{3R} {d{F_g}} = \int\limits_R^{3R} {\dfrac{{GM\lambda }}{{{x^2}}}dx}$ -------- (2)
Integrating equation (2) we get, ${F_g} = \int\limits_R^{3R} {\dfrac{{GM\lambda }}{{{x^2}}}dx} = GM\lambda \left[ {\dfrac{{ - 1}}{x}} \right]_R^{3R}$
On applying the limits we get, ${F_g} = GM\lambda \left[ {\dfrac{{ - 1}}{{3R}} + \dfrac{1}{R}} \right] = \dfrac{{2GM\lambda }}{{3R}}$
Thus the gravitational force acting on the entire stick will be ${F_g} = \dfrac{{2GM\lambda }}{{3R}}$ --------- (3).
Step 3: Express the centripetal force acting on the centre of mass of the stick.
The position of the centre of mass is in the middle of the stick so the centre of mass will be at a distance of $r = 2R$ from the centre of the earth. So the radius of the orbit along which the centre of mass rotates will be $r = 2R$ .
Now if the angular velocity of the stick is $\omega$ and $m = \lambda \left( {2R} \right)$ is the mass of the stick, then the centripetal force will be ${F_c} = m\left( {2R} \right){\omega ^2} = \lambda 4{R^2}{\omega ^2}$ --------- (4).
Also, the centrifugal force and the gravitational force acting on the stick will be balanced.
i.e., ${F_g} = {F_c}$ ------- (5)
Substituting equations (3) and (4) in (5) we get, $\dfrac{{2GM\lambda }}{{3R}} = \lambda 4{R^2}{\omega ^2}$
$\Rightarrow {\omega ^2} = \dfrac{{GM}}{{6{R^3}}}$ and so the angular velocity of the stick will be $\omega = \sqrt {\dfrac{{GM}}{{6{R^3}}}}$ .
Step 4: Express the relation for the period of the orbit of the stick.
The period of revolution of the stick will be $T = \dfrac{{2\pi }}{\omega }$ -------- (6)
Substituting for $\omega = \sqrt {\dfrac{{GM}}{{6{R^3}}}}$ in equation (6) we get, $T = 2\pi \sqrt {\dfrac{{6{R^3}}}{{GM}}}$ .
The acceleration due to gravity on the surface of the earth can be expressed as $g = \dfrac{{GM}}{{{R^2}}}$ .
So the final relation for the period of the orbit will be $T = 2\pi \sqrt {\dfrac{{6R}}{g}}$ .

So the correct option is B.

Note: To evaluate the integral in equation (2) we first take the constants outside the integral to get ${F_g} = GM\lambda \int\limits_R^{3R} {\dfrac{{dx}}{{{x^2}}}}$ . The value of the integral of $\dfrac{1}{{{x^2}}}$ is $\dfrac{{ - 1}}{x}$ and so we obtain ${F_g} = GM\lambda \left[ {\dfrac{{ - 1}}{x}} \right]_R^{3R}$ . The centrifugal force is equal in magnitude to the centripetal force. As the gravitational force and the centrifugal force are balanced, the radius of the orbit along which the centre of mass rotates will be fixed. The gravitational force will be directed inwards while the centrifugal force will be directed outwards.