Question

Consider a vector field $\vec{F} = (2xz + 3y^2)\hat{y} + 4yz^2\hat{z}$. The closed path ($\Gamma$: $A \rightarrow B \rightarrow C \rightarrow D \rightarrow A$) in the $z = 0$ plane is shown in the figure.

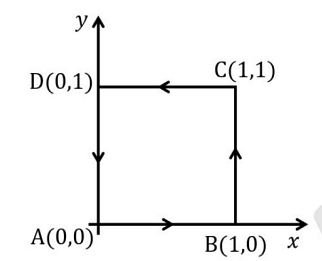
$\oint_\Gamma \vec{F} \cdot d\vec{l}$ denotes the line integral of $\vec{F}$ along the closed path $\Gamma$. Which of the following options is/are true?

• A. $\oint_\Gamma \vec{F} \cdot d\vec{l} = 0$
• B. $\vec{F}$ is non-conservative.
• C. $\vec{\nabla} \cdot \vec{F} = 0$
• D. $\vec{F}$ can be written as the gradient of a scalar field

Answer 1

Answer: (A), (B)

$\oint_\Gamma \vec{F} \cdot d\vec{l} = 0$

Answer 2

The correct Answers are (A):$\oint_\Gamma \vec{F} \cdot d\vec{l} = 0$,(B):$\vec{F}$ is non-conservative.