Question

Consider a uniform square plate of side $a$ and mass $m$. The moment of inertia of this plate about an axis perpendicular to its plane and passing through one of its corner is:
A) $\dfrac{5}{6}m{a^2}$
B) $\dfrac{1}{{12}}m{a^2}$
C) $\dfrac{7}{{12}}m{a^2}$
D) $\dfrac{2}{3}m{a^2}$

Answer 1

To solve this question we have to apply a parallel axis theorem. According to this theorem, the moment of inertia along an axis parallel to the original axis will be the sum of the moment of inertia along the perpendicular axis and the product of mass and the distance between the perpendicular axis and parallel axis.

Formulae used:
${I_{parallel}} = {I_{perpendicular}} + M{R^2}$
Here ${I_{parallel}}$ is the moment of inertia along the parallel axis, ${I_{perpendicular}}$ is the moment of inertia along the axis through the centre of mass, $M$ is the mass of the object and $R$ is the distance between the centre of mass and the parallel axis.

Complete step by step answer:
In the question, a uniform square plate of side $a$ and mass $m$ is given. Let’s draw a figure.

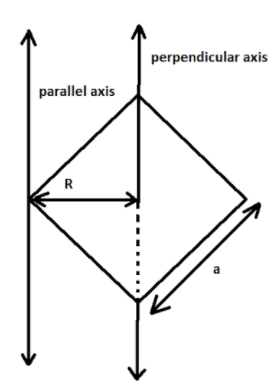
From the above figure, we can easily find $R$ using the Pythagoras theorem,
$\Rightarrow R = \sqrt {{a^2} - {{\left( {\dfrac{a}{2}} \right)}^2}} = \dfrac{a}{{\sqrt 2 }}$
We know that for a square plate, the moment of inertia along a perpendicular axis passing through the centre of mass is,
$\Rightarrow {I_{perpendicular}} = \dfrac{{m{a^2}}}{6}$
So, using the parallel axis theorem, we get
$\Rightarrow {I_{parallel}} = {I_{perpendicular}} + M{R^2}$
Here ${I_{parallel}}$ is the moment of inertia along the parallel axis, ${I_{perpendicular}}$ is the moment of inertia along the axis through the centre of mass, $M$ is the mass of the object and $R$ is the distance between the centre of mass and the parallel axis.
Substituting the value of $R$ and ${I_{perpendicular}}$ we get
$\Rightarrow {I_{parallel}} = {I_{perpendicular}} + M{R^2}$
$\therefore {I_{parallel}} = \dfrac{{m{a^2}}}{6} + \dfrac{{m{a^2}}}{{{{\left( {\sqrt 2 } \right)}^2}}} = \dfrac{2}{3}m{a^2}$

So the required answer is $\dfrac{2}{3}m{a^2}$. Hence option (D) is correct.

Note: While solving questions related to moment of inertia, make sure to apply the correct formulae. There are two different theorems i.e. parallel axis theorem and perpendicular axis theorem. Always use the correct theorem. The parallel axis theorem is used for axes parallel to the centroidal axis of the body. However, the perpendicular axis theorem is used for axes that are perpendicular to the centroidal axis of the body.