Question

Consider a triangle ABC and details regarding it is as given below:
$\Delta ABC$, $a=2$, $b=3$ and $\sin A=\dfrac{2}{3}$. Then, $\cos C$ is equal to
A. $\dfrac{1}{2}$
B. $\dfrac{2}{3}$
C. $\dfrac{2}{\sqrt{3}}$
D. $\dfrac{1}{\sqrt{13}}$

Answer 1

In the question, 2 sides of $\Delta ABC$ and 1 angle is given. We have to find $\cos C$ with the help of trigonometry formulas. We will use sine rule here i.e. $\dfrac{\sin A}{a}=\dfrac{\sin B}{b}=\dfrac{\sin C}{c}$ out of which we will consider $\dfrac{\sin A}{a}=\dfrac{\sin B}{b}$ as per data given.

Complete step-by-step answer:
We are given sides $a=2$, $b=3$ and angle $\sin A=\dfrac{2}{3}$.

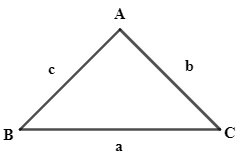
We will use sine rule formula:
$\dfrac{\sin A}{a}=\dfrac{\sin B}{b}=\dfrac{\sin C}{c}$
Let us consider the above triangle with sides a, b, c and the angles as A, B, C. Now, we can look at the sine rule. We know that the sine rule formula is given by sine of angle by opposite side length. So, we can consider first two ratios and can write it as:
$=\dfrac{\sin A}{a}=\dfrac{\sin B}{b}\Rightarrow \dfrac{\dfrac{2}{3}}{2}=\dfrac{\sin B}{3}$
$=\dfrac{2}{6}=\dfrac{\sin B}{3}$
$=\sin B=1$
$\therefore B={{\sin }^{-1}}\left( 1 \right)={{90}^{\circ }}$
$\therefore AngleB={{90}^{\circ }}$
So, diagram will be

Now, we want to find angle $\cos C$, so,
$\cos \theta =\dfrac{\text{Adjacent side}}{\text{Hypotenuse}}$
$\cos C=\dfrac{2}{3}$
Hence, the correct option is (b).

Note: In this, students should know the formula for all the trigonometric ratios. Here, no need to find the third side of the triangle. It is not given in the question that ABC is a right angled triangle, so we cannot directly write that $\sin A=\dfrac{2}{3}$ means 2 is perpendicular and 3 is the hypotenuse, and then try to compute $\cos C$ using this data. This is a very common mistake made by students in the exams. Such silly mistakes must be avoided.