Question

Consider a thremodynamics cycle in a PV diagram shown in the figure performed by one mole of a monoatomic gas. The temperature at A is $T_0$ and volumes are related as $V_B = V_C = 2V_A$. Choose the correct options :-

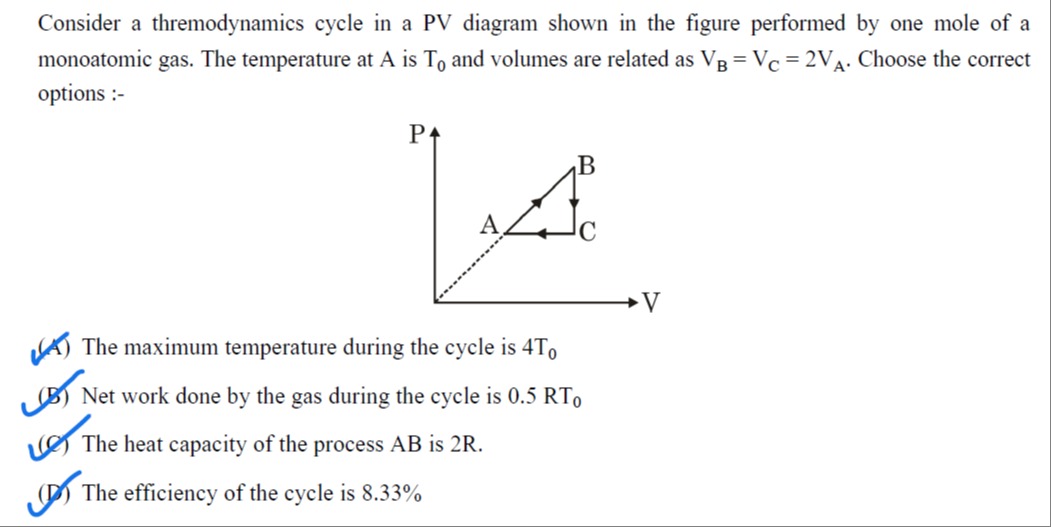
• A. The maximum temperature during the cycle is $4T_0$
• B. Net work done by the gas during the cycle is $0.5 RT_0$
• C. The heat capacity of the process AB is 2R.
• D. The efficiency of the cycle is 8.33%

Answer 1

Answer: (A), (B), (C), (D)

(A), (B), (C), (D)

Answer 2

Let $V_A = V_0$. Then $V_B = V_C = 2V_0$.
Given $T_A = T_0$. For 1 mole of ideal gas, $P_A V_A = RT_A$, so $P_A V_0 = RT_0$, which means $P_A = \frac{RT_0}{V_0}$.
From the diagram, process C to A is isobaric, so $P_C = P_A = \frac{RT_0}{V_0}$.
Process B to C is isochoric, so $V_B = V_C = 2V_0$.
Process A to B is a straight line in the PV diagram. From the dashed line passing through the origin and A, it is implied that the process A to B is of the form $P \propto V$. Let $P = kV$.
At point A, $P_A = kV_A$, so $\frac{RT_0}{V_0} = kV_0$, which gives $k = \frac{RT_0}{V_0^2}$.
So the equation for process A to B is $P = \frac{RT_0}{V_0^2}V$.
At point B, $V_B = 2V_0$, so $P_B = \frac{RT_0}{V_0^2}(2V_0) = \frac{2RT_0}{V_0}$.
The coordinates of the points are:
A: $(V_0, \frac{RT_0}{V_0})$
B: $(2V_0, \frac{2RT_0}{V_0})$
C: $(2V_0, \frac{RT_0}{V_0})$

Temperatures at the points:
$T_A = \frac{P_A V_A}{R} = \frac{(RT_0/V_0)V_0}{R} = T_0$.
$T_B = \frac{P_B V_B}{R} = \frac{(2RT_0/V_0)(2V_0)}{R} = 4T_0$.
$T_C = \frac{P_C V_C}{R} = \frac{(RT_0/V_0)(2V_0)}{R} = 2T_0$.

(A) The maximum temperature during the cycle is $4T_0$.
Process A to B: $T = \frac{PV}{R} = \frac{(RT_0/V_0^2)V \cdot V}{R} = \frac{T_0}{V_0^2} V^2$. As $V$ goes from $V_0$ to $2V_0$, $T$ increases from $T_0$ to $4T_0$.
Process B to C: Isochoric, $V=2V_0$. $P$ changes from $P_B = 2RT_0/V_0$ to $P_C = RT_0/V_0$. Temperature changes from $T_B = 4T_0$ to $T_C = 2T_0$. Temperature decreases linearly with pressure.
Process C to A: Isobaric, $P=RT_0/V_0$. $V$ changes from $V_C = 2V_0$ to $V_A = V_0$. Temperature changes from $T_C = 2T_0$ to $T_A = T_0$. Temperature decreases linearly with volume.
The maximum temperature is $4T_0$ at point B. Option (A) is correct.

(B) Net work done by the gas during the cycle is $0.5 RT_0$.
The net work done is the area enclosed by the cycle in the PV diagram. The cycle is a triangle ABC.
$W_{net} = \text{Area of triangle ABC} = \frac{1}{2} \times \text{base} \times \text{height}$.
Considering the base along the vertical line $V=2V_0$ (from C to B), the base length is $P_B - P_C = \frac{2RT_0}{V_0} - \frac{RT_0}{V_0} = \frac{RT_0}{V_0}$.
The height is the horizontal distance from the line $V=2V_0$ to point A, which is $V_C - V_A = 2V_0 - V_0 = V_0$.
$W_{net} = \frac{1}{2} \times \frac{RT_0}{V_0} \times V_0 = \frac{1}{2} RT_0 = 0.5 RT_0$.
Since the cycle is clockwise, the work done is positive. Option (B) is correct.

(C) The heat capacity of the process AB is 2R.
Process A to B is $P = \frac{RT_0}{V_0^2}V$, which is of the form $P = constant \cdot V$. This can be written as $PV^{-1} = constant$.
For a process $PV^x = constant$, the molar heat capacity is $C = C_V + \frac{R}{1-x}$. Here $x = -1$.
For a monoatomic gas, $C_V = \frac{3}{2}R$.
$C_{AB} = C_V + \frac{R}{1-(-1)} = \frac{3}{2}R + \frac{R}{2} = \frac{4}{2}R = 2R$.
Option (C) is correct.

(D) The efficiency of the cycle is 8.33%.
Efficiency $\eta = \frac{W_{net}}{Q_{in}}$. We need to find the heat absorbed during the cycle.
$W_{net} = 0.5 RT_0$.
Heat absorbed in process A to B: $Q_{AB} = \Delta U_{AB} + W_{AB}$.
$\Delta U_{AB} = C_V (T_B - T_A) = \frac{3}{2}R (4T_0 - T_0) = \frac{3}{2}R (3T_0) = \frac{9}{2}RT_0$.
$W_{AB} = \int_{V_A}^{V_B} P dV = \int_{V_0}^{2V_0} \frac{RT_0}{V_0^2}V dV = \frac{RT_0}{V_0^2} [\frac{V^2}{2}]_{V_0}^{2V_0} = \frac{RT_0}{V_0^2} (\frac{(2V_0)^2}{2} - \frac{V_0^2}{2}) = \frac{RT_0}{V_0^2} (\frac{4V_0^2 - V_0^2}{2}) = \frac{RT_0}{V_0^2} \frac{3V_0^2}{2} = \frac{3}{2}RT_0$.
$Q_{AB} = \frac{9}{2}RT_0 + \frac{3}{2}RT_0 = \frac{12}{2}RT_0 = 6RT_0$. Since $Q_{AB} > 0$, heat is absorbed.

Heat in process B to C: Isochoric, $W_{BC} = 0$. $Q_{BC} = \Delta U_{BC} = C_V (T_C - T_B) = \frac{3}{2}R (2T_0 - 4T_0) = \frac{3}{2}R (-2T_0) = -3RT_0$. Since $Q_{BC} < 0$, heat is released.

Heat in process C to A: Isobaric. $Q_{CA} = C_P (T_A - T_C)$. For monoatomic gas, $C_P = C_V + R = \frac{3}{2}R + R = \frac{5}{2}R$.
$Q_{CA} = \frac{5}{2}R (T_0 - 2T_0) = \frac{5}{2}R (-T_0) = -\frac{5}{2}RT_0$. Since $Q_{CA} < 0$, heat is released.

Total heat absorbed $Q_{in}$ is the sum of positive heat transfers. In this cycle, only process A to B involves heat absorption.
$Q_{in} = Q_{AB} = 6RT_0$.
Efficiency $\eta = \frac{W_{net}}{Q_{in}} = \frac{0.5 RT_0}{6RT_0} = \frac{0.5}{6} = \frac{1}{12}$.
As a percentage, $\eta = \frac{1}{12} \times 100\% = 8.333...\%$.
Option (D) is correct.

Since multiple options are correct, we check all of them. Options (A), (B), (C), and (D) are all correct.