Question

Consider a thin square sheet of side L and thickness t, made of a material of resistivity $\rho$ . The resistance between two opposite faces, shown by the shaded areas in the figure is,

A. Directly proportional to L.
B. Directly proportional to t.
C. Independent of L.
D. Independent of t.

Answer 1

To solve this question, we must know that resistance of a material is directly proportional to the length of the material and inversely proportional to the area of cross section. We will find the area of the cross section for one face and substitute in the equation for resistance. Then we will analyze which of the factors resistance depends upon.
Formula Used:
$R=\rho \dfrac{l}{A}$

Complete answer:
We know that resistance of a conductor is directly proportional to its length and inversely proportional to its area of cross section. That is,
$\begin{aligned} & R\propto \dfrac{l}{A} \\\ & R=\rho \dfrac{l}{A} \\\ \end{aligned}$
Where, $\rho$ is a constant known as resistivity of the material.
Now, we are given with a square sheet of side l.

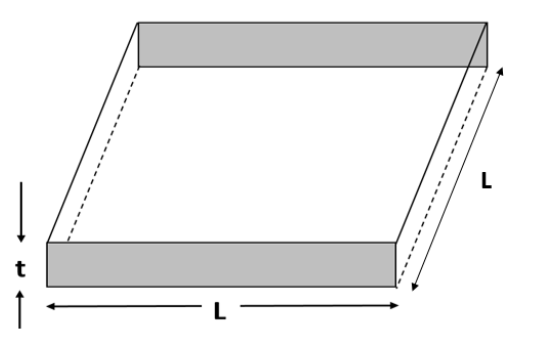
If we take one of the shaded faces,

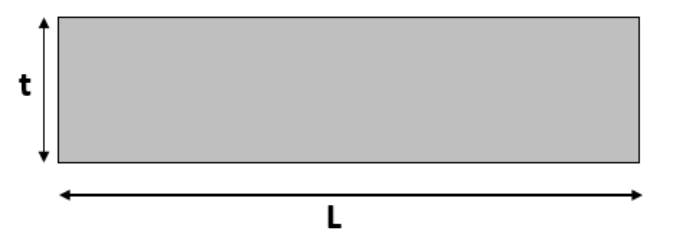
Now, the resistance of this face will be given by,
$R=\rho \dfrac{l}{A}$
Where, l is the length of the conductor and A is the area of cross section.
Here, the area of the cross section of one face can be found by taking the product of length and thickness of the sheet. That is,
$A=L\times t$
Now, we will substitute this area in the equation for resistance.
$\begin{aligned} & R=\rho \dfrac{l}{A} \\\ & \Rightarrow R=\rho \dfrac{L}{L\times t} \\\ & \therefore R=\dfrac{\rho }{t} \\\ \end{aligned}$
So, the resistance of one face of the sheet is equal to $\dfrac{\rho }{t}$. That is,
$R\propto \dfrac{1}{t}$
This will be true for all four cases of the square sheet. So, the resistance between two faces of the square sheet is inversely proportional to its thickness only.

Therefore, option C is correct.

Note:
We must know that resistivity of a conductor is defined as the resistance of a conductor of unit cross sectional area and unit length. Also, resistivity of a conductor only changes according to the material of the conductor. It can be found using the formula,
$\rho =\dfrac{RA}{l}$