Question
Question: Consider a thin metallic sheet perpendicular to the plane of the paper moving with speed \('v'\) in ...
Consider a thin metallic sheet perpendicular to the plane of the paper moving with speed ′v′ in a uniform magnetic field B going into the plane of the paper (See figure). If charge densities σ1 and σ2 are induced on the left and right surfaces, respectively, on the sheet then (ignore fringe effects):
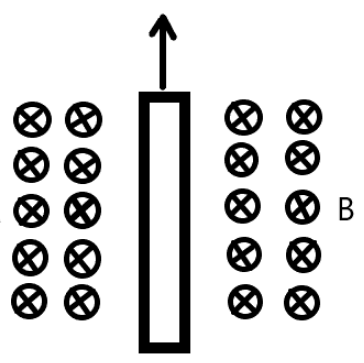
A. σ1=2−ε0vB , σ2=2ε0vB
B. σ1=ε0vB , σ2=−ε0vB
C. σ1=2ε0vB , σ2=2−ε0vB
D. σ1=σ2=ε0vB
Solution
Here, we will use the force formula in case of both electric field and magnetic field. The system will be in equilibrium because the charge on both the left and right side will be the same. Therefore, we will equate the forces in both the cases to calculate the charge densities.
Complete step by step answer:
The following terms are given in the question,
Speed of metallic sheet =v.
Magnetic field induced in the plane of paper =B.
Charge densities that are induced in the plane of paper =σ1andσ2.
Now, as the charge is moving, it will induce a magnetic field B in the plane of the paper.
Now, the force acting on the charges is given below,
F1=qE
Here, E is the electric field and is shown as E=ε0σ
Now, the force due to magnetic field B is given below,
F2=q(v×B)
As given in the question, v is perpendicular to B , therefore, the angle between them is 90∘ . Therefore, the above equation will become
F2=qvBsin90∘
⇒F2=qvB
As we know that the charges are induced on the same material, therefore, σ1=σ2 but the charges will be opposite. Also, we know that the velocity is acting upwards than σ1 will be positive and σ2 will be negative.
Now, at equilibrium, F1=F2
qE=qvB
⇒E=vB
⇒ε0σ=vB
⇒σ=ε0vB
Now, as discussed above, σ1 will be positive and σ2 will be negative.
∴σ1=ε0vB and σ2=−ε0vB
Therefore, charge densities σ1 and σ2 induced on the sheets are ε0vB and −ε0vB respectively.
Hence, option B is the correct option.
Note: We have forces in case of electric field and magnetic field because the charges are moving and will produce both the electric field and magnetic field. Also, charge densities are of opposite signs because the velocity of the charge is in upward direction. Also, it is given in the question that the plane of paper is perpendicular to the metallic sheet.
