Question
Question: Consider a tank made of glass (refractive index \( 1.5 \) ) with a thick bottom. It is filled with a...
Consider a tank made of glass (refractive index 1.5 ) with a thick bottom. It is filled with a liquid of refractive index μ . A student finds that, irrespective of what the incident angle i (see figure) is for a beam of light entering the liquid, the light reflected from the liquid glass interface is never completely polarized. For this to happen, the minimum value of μ is
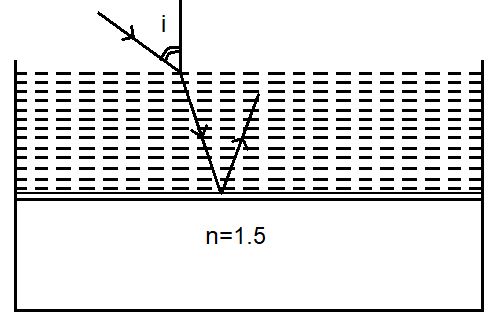
(A) 53
(B) 35
(C) 35
(D) 34
Solution
For finding out the minimum value of the refractive index, we need to use the relation between Brewster angle and the critical angle which is given as sin c<sin ib . Brewster angle is an angle of incidence at which light with a particular polarization is perfectly transmitted through a transparent dielectric surface, with no reflection.
Formula used:
sin c<sin ib
sin90=μsinc ⇒sinc=μ1
Where, the critical angle be c , the Brewster angle be ib , μ is the refractive index.
Complete step by step solution:
Let us consider the critical angle be c, the Brewster angle be ib.
The relation comes between the critical angle and the Brewster angle is,
sin c<sin ib
For the ray travelling from air to liquid,
sin90=μsinc
Now the value of sin90 is 1 so we get
sinc=μ1
Since, we know that,
tanib=μ0rel
And,
sin c<sin ib
Then substituting the values in the equation we get,
⇒μ1<μ2+(1.5)21.5
Thus, after simplification, we get,
⇒μ<53
Hence, the correct answer is option A.
Note:
There are numerous applications of Brewster angle in real life. It includes,
-Polarized sunglasses use the principle of Brewster's angle to reduce glare from the sun reflecting off horizontal surfaces such as water or road.
-Photographers use the same principle to remove reflections from water so that they can photograph objects beneath the surface.
-Brewster angle prisms are used in laser physics. The polarized laser light enters the prism at Brewster's angle without any reflective losses.
-In surface science, Brewster angle microscopes are used in imaging layers of particles or molecules at air-liquid interfaces.
