Question

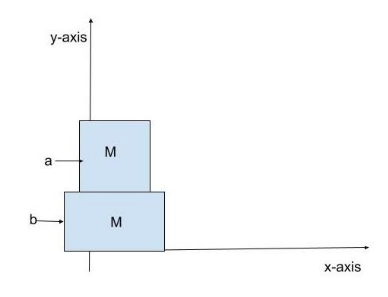
Consider a system of 2 boxes, each with mass M, which are stacked as shown in the diagram. The top box has height “a” and the bottom height “b”. At what y-coordinate is the system's centre of mass located, if the bottom of the lower box is at $y = 0$ ? Assume both boxes have uniform density (the centre of mass of each box is located at its centre).

A. $\dfrac{1}{4}\left( {a + 4b} \right)$
B. $\dfrac{1}{2}a$
C. $\dfrac{1}{2}\left( {a + 3b} \right)$
D. $\dfrac{1}{2}\left( {a + b} \right)$
E. $\dfrac{1}{4}\left( {a + 3b} \right)$

Answer 1

The centre of mass of a mass distribution in space is the unique point in space where the weighted relative position of the distributed mass sums to zero, according to physics. A force can be applied to this point to cause a linear acceleration without causing an angular acceleration.

Complete step by step answer:
For the purpose of calculating the "first moment," i.e., mass times distance, the centre of mass is the point at which all of the mass can be considered "concentrated." The centroid or geometric centre of a flat shape is the arithmetic mean position of all the points in the figure in mathematics and science. Informally, it's the point at which a perfectly balanced cut out of the shape could be balanced on the tip of a pin.

Now coming to the question;
Given: ${m_1} = {m_2} = M$
A block's geometric centre is where its centre of mass is located.
From figure, ${y_1} = \dfrac{b}{2}$
${y_2} = b + \dfrac{a}{2} = \dfrac{{2b + a}}{2}$
Using,
${y_{cm}} = \dfrac{{{m_1}{y_1} + {m_2}{y_2}}}{{{m_1} + {m_2}}} \\\ \Rightarrow {y_{cm}} = \dfrac{{M\left( {\dfrac{b}{2}} \right) + M\left( {\dfrac{{2b + a}}{2}} \right)}}{{M + M}} \\\ \therefore {y_{cm}} = \dfrac{{a + 3b}}{4} \\\$
Hence, the correct option is E.

Note: The centre of mass is a useful reference point for mechanics calculations involving masses scattered in space, such as planetary bodies' linear and angular momentum and rigid body dynamics. The equations of motion of planets are stated as point masses centred at the centres of mass in orbital mechanics. The centre of mass frame is an inertial frame in which a system's centre of mass is at rest with relation to the coordinate system's origin.