Question

Consider a spherical gaseous cloud of mass density $\rho \left( r \right)$ in a free space where $r$ is the radial distance from its centre. The gaseous cloud is made of particles of equal mass $m$ moving in circular orbits about their common centre with the same kinetic energy $K$. The force acting on the particle is their mutual gravitational force. If $\rho \left( r \right)$ is constant in time. The particle number density $n\left( r \right) = \rho \left( r \right)/m$ is? ($G =$ universal gravitational constant)
(A) $\dfrac{K}{{6\pi {r^2}{m^2}G}}$
(B) $\dfrac{K}{{\pi {r^2}{m^2}G}}$
(C) $\dfrac{{3K}}{{\pi {r^2}{m^2}G}}$
(D) $\dfrac{K}{{2\pi {r^2}{m^2}G}}$

Answer 1

To solve this question, we need to find out the gravitational force on a particle as a function of the distance from the centre. This has to be equated with the centripetal force on the particle. On differentiating the equation obtained with respect to the radial distance, we will get the required expression for the number density.

Formula Used: We will be using the following formula here,
$F = \dfrac{{GmM}}{{{r^2}}}$ where $F$ is the gravitational force, $G$ is the universal gravitational constant, $m,M$ are the masses and $r$ is the distance.
${F_c} = \dfrac{{m{v^2}}}{r}$ where ${F_c}$ is the centripetal force and $v$ is the velocity.

Complete step-by-step solution:
Consider one particle of mass $m$ moving with a velocity of $v$ on the circumference of a hollow sphere of radius $r$ and of thickness $dr$ inside the given sphere as shown in the figure.

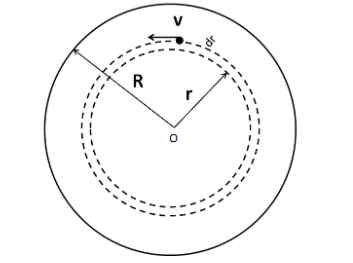
The small mass of this hollow sphere can be written as
$dM = \rho \left( r \right)dV$...........................(1)
We know that the volume of a sphere is given by
$V = \dfrac{4}{3}\pi {r^3}$
Differentiating both sides with respect to $r$ we get
$dV = 4\pi {r^2}dr$
Putting this in (1) we get
$dM = 4\pi {r^2}\rho \left( r \right)dr$....................(2)
Now, from the shell theorem, for the particle situated on the sphere, the whole mass of the sphere and its inside region can be taken at its centre O. So the force on the particle can be written as
$F = \dfrac{{GmM}}{{{r^2}}}$.....................(3)
As the particle is rotating with a speed of $v$, so this force must be equal to the centripetal force, which can be given by
${F_c} = \dfrac{{m{v^2}}}{r}$...............................(4)
Equating (3) and (4) we get
$\dfrac{{m{v^2}}}{r} = \dfrac{{GmM}}{{{r^2}}}$..........................(5)
Now, the kinetic energy of the particle is
$K = \dfrac{1}{2}m{v^2}$
$\Rightarrow m{v^2} = 2K$
Substituting this in (5) we get
$\dfrac{{2K}}{r} = \dfrac{{GmM}}{{{r^2}}}$
$\Rightarrow M = \dfrac{{2Kr}}{{Gm}}$
Differentiating both sides with respect to $r$ we get
$\dfrac{{dM}}{{dr}} = \dfrac{{2K}}{{Gm}}$
$\Rightarrow dM = \dfrac{{2K}}{{Gm}}dr$
Substituting (2) above, we get
$4\pi {r^2}\rho \left( r \right)dr = \dfrac{{2K}}{{Gm}}dr$
$\Rightarrow \rho \left( r \right) = \dfrac{K}{{2\pi {r^2}mG}}$........................(6)
The number density is
$n\left( r \right) = \dfrac{{\rho \left( r \right)}}{m}$
Putting (6) in above equation
$n\left( r \right) = \dfrac{K}{{2\pi {r^2}{m^2}G}}$

Hence, the correct answer is option D.

Note: We should not be confused as to why we haven’t considered the mass of the region outside the spherical shell. From the shell theorem, the force of attraction due to a hollow spherical shell on a point mass inside it is equal to zero.