Question

Consider a spherical drop of radius R. Surface tension of the liquid is S. Force of the surface tension on the shaded sub hemisphere due to remaining drop is $\dfrac{{S\pi R}}{2}$. The value of angle $\theta$ (angle subtended by the sub hemisphere at centre of drop) is

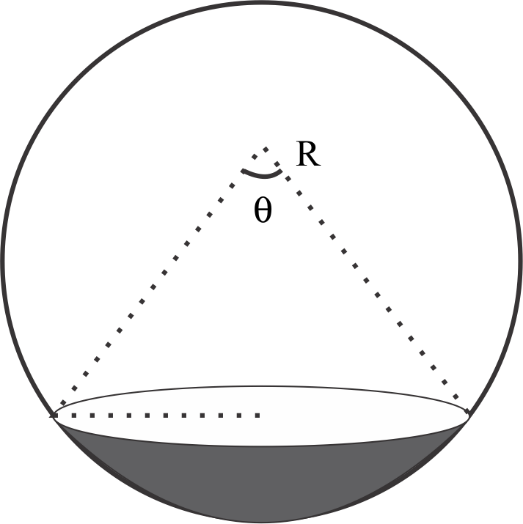
(A) $60^\circ$
(B) $120^\circ$
(C) $30^\circ$
(D) $90^\circ$

Answer 1

Hint We are provided with the force of the surface tension on the shaded sub hemisphere due to the remaining drop being $\dfrac{{S\pi R}}{2}$. We can understand that statement from the diagram in the question. We have to find the angle subtended by the sub hemisphere at centre of drop. Use the surface tension formula to find the angle. Since the given surface is a sphere its radius makes an angle with the centre point. Use the given diagram for better understanding.

Complete step by step answer
Surface tension: The tendency of surfaces to shrink into the possible minimum surface area. The surface tension is the force per unit length of the surface. Surface area of an object is given by
$\Rightarrow \gamma = \dfrac{F}{l}$
$\gamma$ is the surface tension
F is the force
L is the unit length
Given,
The radius of a spherical drop is R
Surface tension of the liquid is S
Force of the surface tension on the shaded sub hemisphere due to remaining drop is $F = \dfrac{{S\pi R}}{2}$.
Angle subtended by the sub hemisphere at centre of drop $\theta = ?$

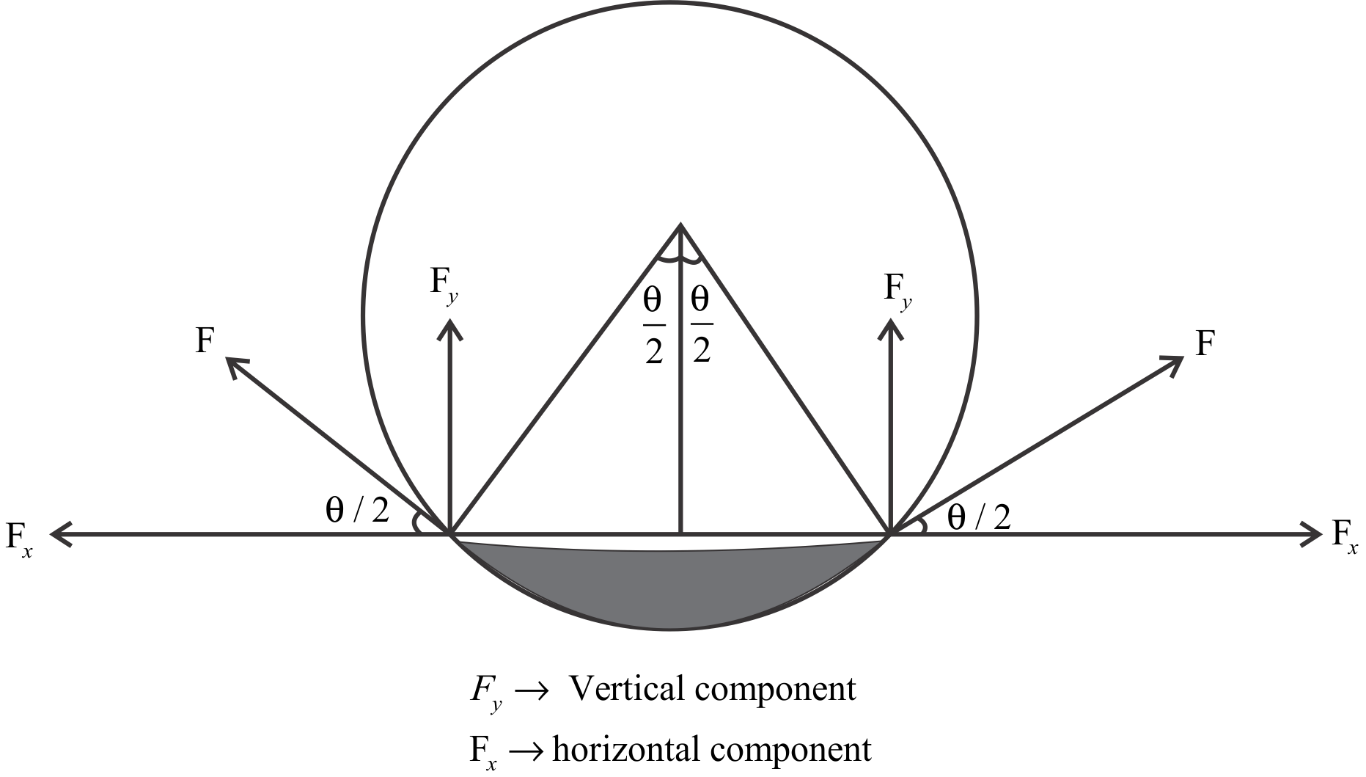
We know that
$\Rightarrow \gamma = \dfrac{F}{l}$
$\Rightarrow F = \gamma \times l$
Substituting the known values,
$\Rightarrow F = \gamma \times l$
$\Rightarrow F = S \times 2\pi R$
From the diagram
$\Rightarrow F = S \times 2\pi R\sin \dfrac{\theta }{2}{\text{ }} \to {\text{1}}$
From the diagram,
All the horizontal components of the force get cancelled.
The net force by vertical component of force
$\Rightarrow F = F\sin \dfrac{\theta }{2}$
Given $F = \dfrac{{S\pi R}}{2}$
$\Rightarrow \dfrac{{S\pi R}}{2} = F\sin \dfrac{\theta }{2}$
From equation 1
$\Rightarrow \dfrac{{S\pi R}}{2} = S \times 2\pi R\sin \dfrac{\theta }{2} \times \sin \dfrac{\theta }{2}$
$\Rightarrow \dfrac{{S\pi R}}{2} = S \times 2\pi R{\sin ^2}\dfrac{\theta }{2}$
$\Rightarrow \dfrac{1}{2} = \times 2{\sin ^2}\dfrac{\theta }{2}$
$\Rightarrow {\sin ^2}\dfrac{\theta }{2} = \dfrac{1}{4}$
Taking square root
$\Rightarrow \sin \dfrac{\theta }{2} = \dfrac{1}{2}$
$\Rightarrow \dfrac{\theta }{2} = {\sin ^{ - 1}}\dfrac{1}{2}$
$\Rightarrow \dfrac{\theta }{2} = 30^\circ$
$\Rightarrow \theta = 60^\circ$
Angle subtended by the sub hemisphere at centre of drop, $\theta = 60^\circ$

Hence the correct answer is option (A) $60^\circ$

Note We can notice that we have used $2\pi R$ in place of L while solving. Surface tension is the force per unit length. Here we are provided with a sphere. To find the surface tension on the sphere we have to use the circumference of the sphere. Circumference of the sphere is $2\pi R$.