Question
Question: Consider a solid sphere of radius R which has volume charge density given by the expression $\rho = ...
Consider a solid sphere of radius R which has volume charge density given by the expression ρ=ρ0(1−Rr) where ρ0 is a constant and r is the distance from the center. There is no charge outside the sphere. Consider potential at infinite distance from the solid sphere to be zero. What is the distance of a point from center of solid sphere where electric field is maximum?
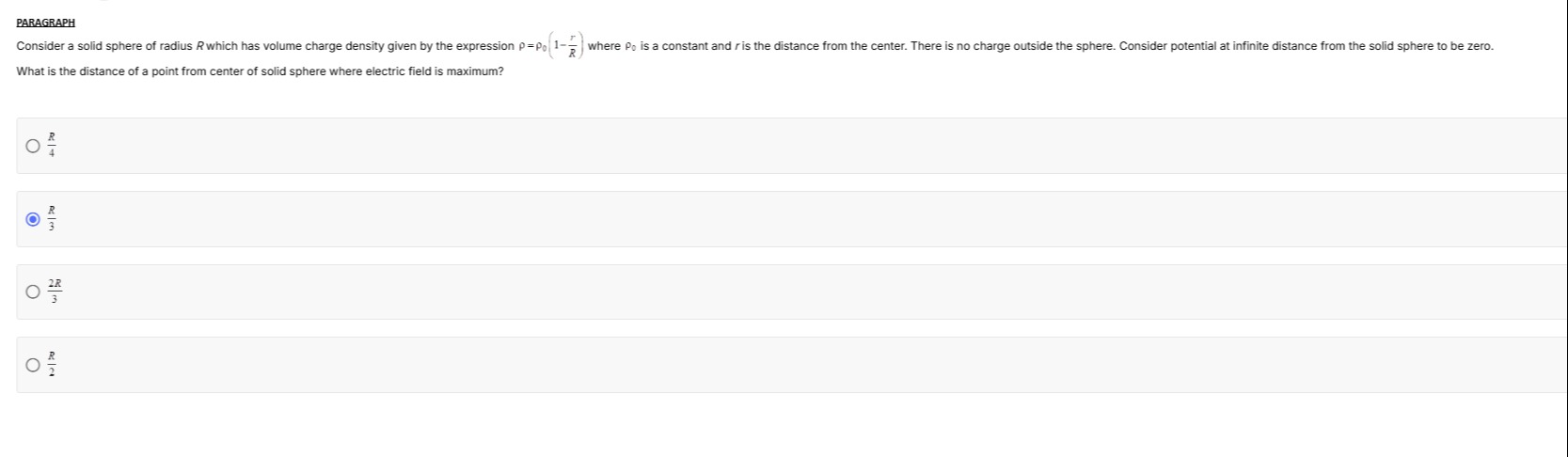
4R
3R
32R
2R
32R
Solution
To find the point where the electric field is maximum, we need to:
-
Calculate the electric field inside the sphere (r≤R) using Gauss's Law. This involves finding the enclosed charge Qenclosed(r) and then applying Gauss's Law to find E(r).
-
Calculate the electric field outside the sphere (r>R) using Gauss's Law with the total charge Qtotal.
-
Find the maximum of E(r) within the sphere (0≤r≤R) by taking the derivative of E(r) with respect to r, setting the derivative to zero, and solving for r.
-
Compare the value of E(r) at the critical point found in step 3 with the value at the boundary r=R and consider the behavior for r>R to determine the absolute maximum.
The electric field is maximum at r=32R.
