Question
Question: Consider a small water drop in air. Let T be the surface tension of water. The figure shows a small ...
Consider a small water drop in air. Let T be the surface tension of water. The figure shows a small section ABC of the drop subtending angle 20 at the centre O. The force due to surface tension acting on this section is.
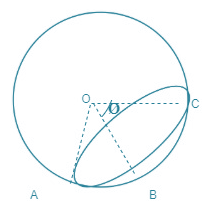
(A) 2 !!π!! TR sin3 !!θ!!
(B) 4 !!π!! TR sin !!θ!!
(C) 2 !!π!! TR sin2 !!θ!!
(D) 2 !!π!! TR sin !!θ!!
Solution
Surface tension is the tendency of liquid surfaces to shrink into the minimum surface area possible.
S.I. unit=newton per meter
(S) Surface tension =LengthForce
The general formula for measuring surface tension is ‘S’ surface tension is equal to force divided by length. The forces behind the origin of surface tension are cohesive force and adhesive force.
Complete step by step solution
To find out the force due to surface tension action on this section, first of all we have to find out the surface area of the hemisphere.
Surface area of hemisphere = !!π!! BC2 ….. (1)
To find out the value of BC, we will
!!θ!! =OCBC[∴ Sin !!θ!! =HP] !!θ!! = rBC !!θ!! r Sin Sin BC=Sin
Putting the value of BC in the equation …. (1)
Surface area = !!π!! (Sin !!θ!! r)2
= !!π!! Sin2 !!θ!! r2 =r2Sin2 !!θ!!
Excess pressure inside an droplet
△P=R2T
But physically, the Pressure is given by
△P=AreaForce
Putting all the value in this expression
Force =△P×Area
=R2T× !!π!! R2Sin2 !!θ!!
F=2 !!π!! T R Sin2 !!θ!!
This is the force due to surface tension acting on this section
So option (C) is correct.
Note
The surface tension of water provides the necessary wall tension for the formation of bubbles with water. High surface tension of water is also the reason why rain comes down as a spherical drop. High surface energy drives water drops to take shape with as little surface area as possible, making sphere shape most favourable.
