Solveeit Logo
Login

Question

Physics Question on speed and velocity

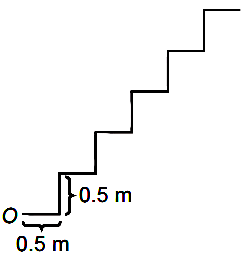
Consider a series of steps as shown. A ball is thrown from 0. Find the minimum speed to directly jump to 5th step
Figure

A

5(2+1)m/s5(\sqrt2+1) m/s

B

5(2)m/s5(\sqrt2) m/s

C

5((2+1))m/s5(\sqrt{(\sqrt2+1))} m/s

D

6(3+1)m/s6(\sqrt3+1) m/s

Answer

5((2+1))m/s5(\sqrt{(\sqrt2+1))} m/s

Explanation

Solution

The Correct option is (C): 5((2+1))m/s5(\sqrt{(\sqrt2+1))} m/s
y=xtan⁡θ−gx22v2cos⁡2θy=x\tan\theta-\frac{gx^2}{2v^2\cos^2\theta}
(2.5,2.5) must lie on this
⇒1=tan⁡θ−g×2.52v2cos⁡2θ⇒1=\tan\theta-\frac{g\times2.5}{2v^2\cos^2\theta}
⇒252v2cos⁡2θ=tan⁡θ−1⇒ \frac{25}{2v^2\cos^2\theta}=\tan\theta-1
⇒ v^2=\frac{25}{2}\left\\{\frac{1+\tan^2\theta}{\tan\theta-1}\right\\}
⇒vmin=52+1⇒ v_{min}=5\sqrt{\sqrt2+1}
[ Happens when tan⁡θ=2+1\tan\theta=\sqrt2+1 ]