Question

Consider a sequence $\{a_n\}$ with $a_1=2$ and $a_n = \frac{a_{n-1}^2}{a_{n-2}}$ (for all $n \ge 3$, terms of the sequence being distinct).

Given that $a_2$ and $a_5$ are positive integers and $a_5 \le 162$ then the possible value(s) of $a_5$ can be

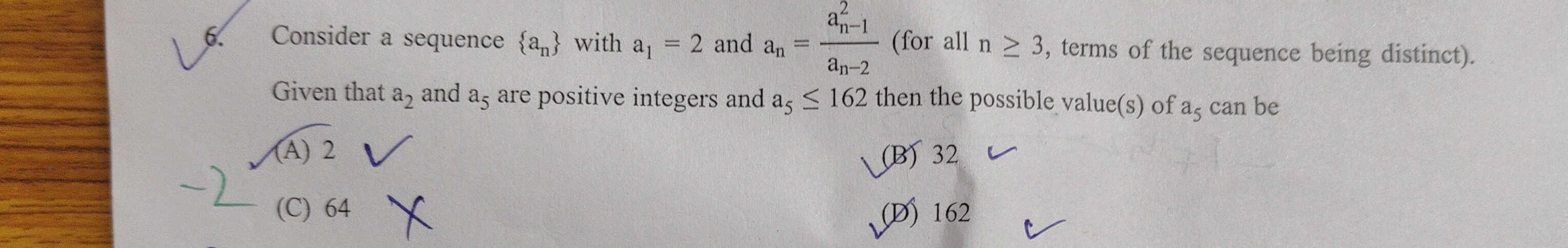
• A. 2
• B. 32
• C. 64
• D. 162

Answer 1

Answer: (B), (D)

32, 162

Answer 2

The recurrence relation $a_n = \frac{a_{n-1}^2}{a_{n-2}}$ implies that the sequence $\{a_n\}$ is a Geometric Progression (GP). Given $a_1 = 2$, we have $a_n = 2r^{n-1}$, where $r$ is the common ratio. Since $a_2 = 2r$ and $a_5 = 2r^4$ are positive integers, let $2r = k$, where $k$ is a positive integer. Thus, $r = \frac{k}{2}$. Substituting this into $a_5$, we get $a_5 = 2(\frac{k}{2})^4 = \frac{k^4}{8}$. For $a_5$ to be an integer, $k^4$ must be divisible by 8, implying $k$ is even. Let $k = 2m$, where $m$ is a positive integer. Then $a_5 = \frac{(2m)^4}{8} = 2m^4$. Given $a_5 \le 162$, we have $2m^4 \le 162$, so $m^4 \le 81$. Possible values for $m$ are 1, 2, and 3.

• If $m=1$, $a_5 = 2(1)^4 = 2$. Then $r = \frac{2(1)}{2} = 1$. The sequence becomes $2, 2, 2, ...$, which violates the distinct terms condition.
• If $m=2$, $a_5 = 2(2)^4 = 32$. Then $r = \frac{2(2)}{2} = 2$. The sequence becomes $2, 4, 8, 16, 32, ...$, which has distinct terms.
• If $m=3$, $a_5 = 2(3)^4 = 162$. Then $r = \frac{2(3)}{2} = 3$. The sequence becomes $2, 6, 18, 54, 162, ...$, which has distinct terms.

Therefore, the possible values of $a_5$ are 32 and 162.