Question
Question: Consider a rubber ball freely falling from a height \[h = 4.9m\] onto a horizontal elastic plate. As...
Consider a rubber ball freely falling from a height h=4.9m onto a horizontal elastic plate. Assume that the duration of collision is negligible and the collision with the plate is totally elastic. Then the velocity as a function of time and the height as a function of time will be
(A) 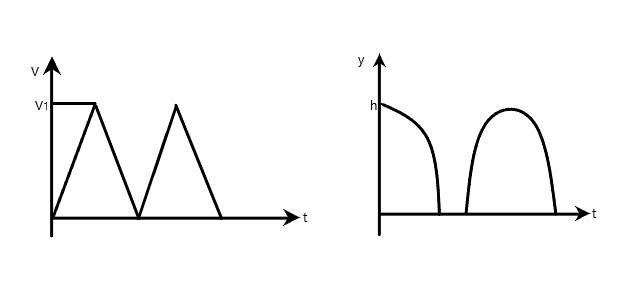
(B) 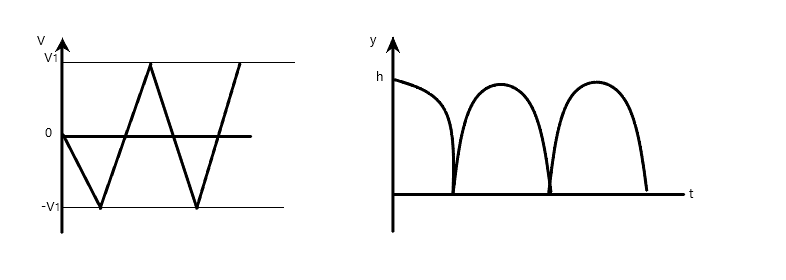
(C) 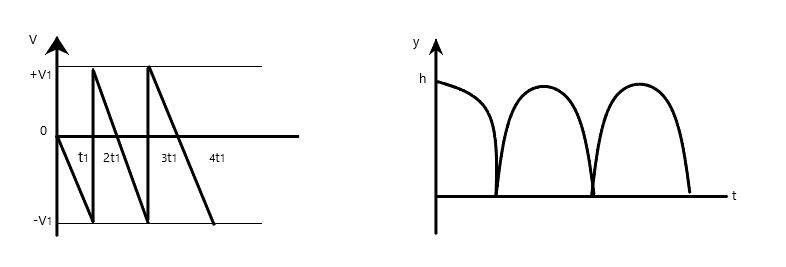
(D) 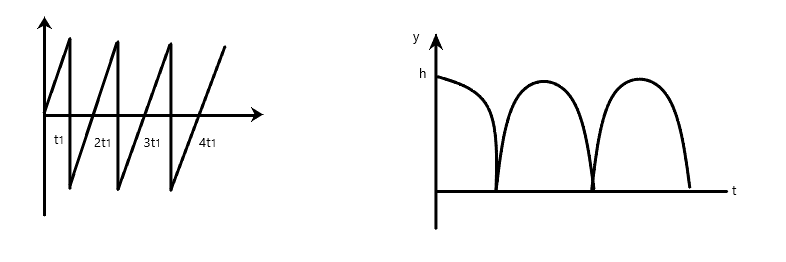
Solution
The statement “assume that the duration of collision is negligible” implies that there is no time lapse between successive bounces. This also implies that the ball velocity reverses direction instantly after it hits the ground. Also, for perfectly elastic collision, the velocity just before the ball hits the ground is equal to its velocity just after it hits the ground. Also, the velocity just before the ball hits the ground is equal to its velocity just after it hits the ground.
Complete Step-by-Step solution:
To answer this question, first let us examine the behavior of the bouncing rubber ball.
When a ball is dropped from height h the velocity of the ball increases linearly downwards, at rate of acceleration due to gravity. It gets to a maximum just before it hits the ground, and reverses direction immediately it hits the ground, and since it is elastic, the velocity just after it hits the ground is equal to the velocity just before it hits the ground, after hitting the ground the velocity decreases upwards, and reaches zero at maximum height, after which increases downward again. Then the cycle continues. The distance on the other hand decreases parabolically downwards, then increases immediately upwards after bouncing. The cycle continues.
To determine the answer we must examine each options against the behavior described above one after the other.
For option A, we easily see that this is not the solution because there is a time lapse between successive bounces as very evident in the distance time-graph.
Option B is a little tricky in that, although the distance-time graph showed no elapsed time between successive bounces, the velocity-time graph showed otherwise.
Observing the velocity-time graph, we see that initially, the velocity starting from zero increases downward which reflects by becoming more negative, as should be the case. However, during the reversal of direction it showed a time lapse as evident in the slanted nature of the lines going from −V1to +V1. Thus, option B is not the correct option.
In option C, we see also that the velocity starting from zero increases downward (velocity becoming more negative). Then increases very steeply from −V1 to +V1 which occurs after collision with the ground. Then the positive velocity reduces until it reaches zero, which corresponds with the ball rising from ground to maximum height. Then the velocity starts to increase downward again, and the cycle continues. This perfectly corresponds with the description above.
Thus, option C is the correct option.
For completeness, option D is incorrect because it shows that the velocity increases upwards after dropping the ball which is incorrect.
Note: The sign convention for velocity (that downward velocity is negative, and upward velocity positive) was not simply a matter of choice. It was chosen with respect to the chosen convention for the distance. From the graphs we see that a decreasing height travels towards the negative y-axis (and an increasing height to the positive y-axis). Thus, during the descent, at a time t2>t1, we have y2<y1. Therefore, for the average velocity for this period, we have that v=t2−t1y2−y1 which is negative since y2<y1and t2>t1.
