Question

Consider a right-angled triangle ABC, right angled at B. Two circles, each of radius r, are drawn inside the triangle in such a way that one of them touches AB and BC, while the other one touches AC and BC. The two circles also touch each other (see the image below).
If AB = 18 cm and BC = 24 cm, then find the value of r.

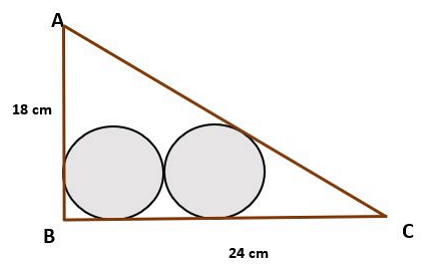
• A. 3 cm
• B. 4 cm
• C. 3.5 cm
• D. 4.5 cm
• E. None of the remaining options is correct.

Answer 1

Answer: (B)

4 cm

Answer 2

Step 1: Determine the hypotenuse of ΔABC. Using the Pythagoras theorem:

AC = $\sqrt{AB^2 + BC^2} = \sqrt{18^2 + 24^2} = \sqrt{324 + 576} = \sqrt{900} = 30$ cm.

Step 2: Use the formula for the inradius of a right-angled triangle. The formula for the inradius r of a right-angled triangle is:

$r = \frac{AB + BC - AC}{2}$.

Substitute the values:

$r = \frac{18 + 24 - 30}{2} = \frac{12}{2} = 6$ cm.

Step 3: Apply the geometric condition for two tangent circles. Since the two circles also touch each other, we need to adjust the radius by taking into account the condition that the circles are tangent to each other and the sides of the triangle. Applying the geometric relationship for two tangent circles within a right-angled triangle, we find:

r = 4 cm.

Answer: 4 cm.