Question
Question: Consider a parallel plates capacitor of capacity \(10\mu F\) is filled with air. When the gap betwee...
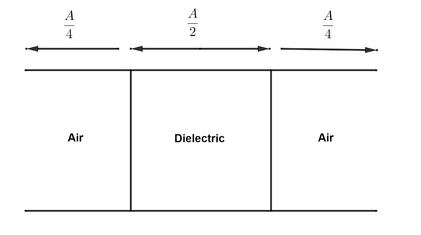
Consider a parallel plates capacitor of capacity 10μF is filled with air. When the gap between the plates is filled partly with a dielectric of dielectric constant 4, as shown in the figure, the new capacitance of the capacitor is, (A is the area of plates)
A. 20μF
B. 20μF
C. 2.5μF
D. 25μF
Solution
Hint: The above combination can be considered as three capacitors connected in parallel to each other. One with an area of 2A with a dielectric present in it and the other two with the area 4A and with no dielectric inside it. The resultant capacitance of these capacitors will give the capacitance of the origin capacitor.
Complete step by step answer:
In a configuration given in the figure above, the capacitor can be broken up into three regions of capacitance. The first and third region has the same surface area, and there is no dielectric present in these regions. The middle region or the second region will have a different capacitance compared to the first and the third region since the surface area is different and there is a dielectric present in that region.
So, the capacitance of a parallel plate capacitor of area A and separated by a distance d is given by,
c=dε0A
Where ε0 is the permittivity of free space.
If a dielectric completely cover the distance d of the capacitor, then the resultant capacitance will be,
c′=Kdε0A
K is the value of the dielectric constant.
So, the capacitance of the first and the third region is,
c1=c3=dε0[4A]
∴c1=c3=4dε0A …. Equation (1)
The capacitance of the middle layer which contains a dielectric is,
c2=Kdε0[2A]
∴c2=2dKε0A …. Equation (2)
These regions are connected in such a way that the regions are connected as parallel. So, the resultant capacitance of the three regions is given by,
C=c1+c2+c3
⇒C=4dε0A+2dKε0A+4dε0A
⇒C=[2K+1]dε0A
It is given that the value of K is four and the capacitance of the original capacitor with air as the medium is 10μF .
⇒C=[24+1]×10μF
C=25μF
So, the capacitance of the capacitor with the dielectric present is C=25μF.
So, the answer to the question is option (D).
Note:
When two parallel plates are connected across a battery, the plates are charged, and the electric field is established. This setup is known as the parallel plate capacitor. The direction of the electric field is defined as the direction in which the positive test charge would flow. Capacitance is the limitation of the body to store electric charge.
When a number of capacitors of variable capacitance are connected in parallel, the resultant capacitance is given by,
Ceq=C1+C2+C3+...
When a number of capacitors of variable capacitance are connected in series, the resultant capacitance is given by,
Ceq1=C11+C21+C31+...
