Question

Consider a matrix $A = [a_{ij}]_{3 \times 3}$, where $a_{ij} = \begin{cases} i-j, & \text{if} \quad ij = \text{odd}\\ i^2, & \text{if} \quad ij = \text{even}. \end{cases}$

If $b_{ij}$ is cofactor of $a_{ij}$ in matrix A and $d_{ij} = \sum_{k=1}^{3} a_{ik}b_{jk}$, then the value of $\sqrt[3]{\det(d_{ij})}$ is equal to

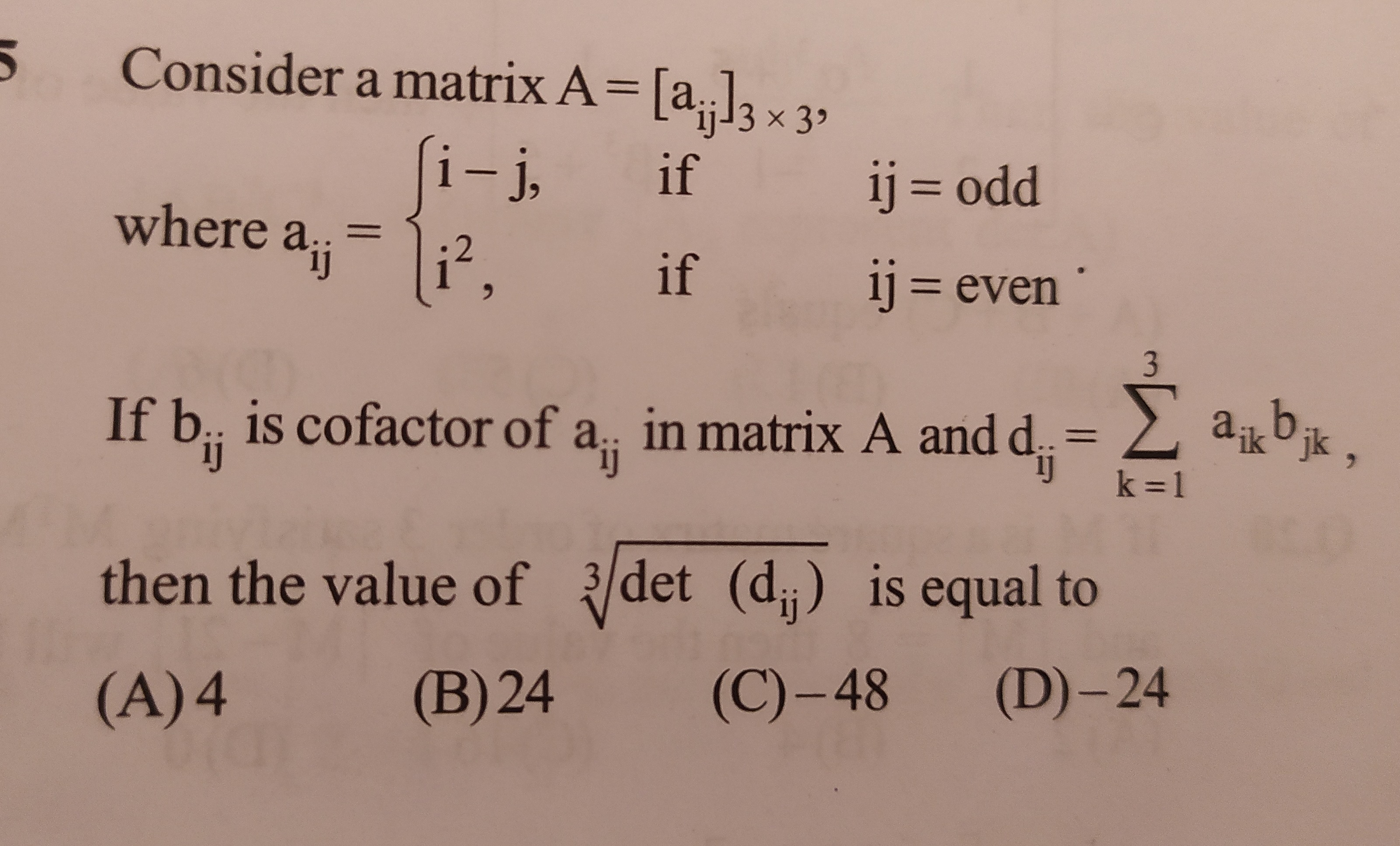
• A. 4
• B. 24
• C. -48
• D. -24

Answer 1

Answer: (C)

-48

Answer 2

The matrix A is given by $A = [a_{ij}]_{3 \times 3}$, where $a_{ij} = \begin{cases} i-j, & \text{if} \quad ij = \text{odd}\\ i^2, & \text{if} \quad ij = \text{even}. \end{cases}$

Let's determine the elements of the matrix A: The product $ij$ is odd if and only if both $i$ and $j$ are odd. The product $ij$ is even if either $i$ or $j$ (or both) is even.

For $i=1$: $a_{11}$: $1 \times 1 = 1$ (odd). $a_{11} = 1-1 = 0$. $a_{12}$: $1 \times 2 = 2$ (even). $a_{12} = 1^2 = 1$. $a_{13}$: $1 \times 3 = 3$ (odd). $a_{13} = 1-3 = -2$.

For $i=2$: $a_{21}$: $2 \times 1 = 2$ (even). $a_{21} = 2^2 = 4$. $a_{22}$: $2 \times 2 = 4$ (even). $a_{22} = 2^2 = 4$. $a_{23}$: $2 \times 3 = 6$ (even). $a_{23} = 2^2 = 4$.

For $i=3$: $a_{31}$: $3 \times 1 = 3$ (odd). $a_{31} = 3-1 = 2$. $a_{32}$: $3 \times 2 = 6$ (even). $a_{32} = 3^2 = 9$. $a_{33}$: $3 \times 3 = 9$ (odd). $a_{33} = 3-3 = 0$.

So, the matrix A is: $A = \begin{pmatrix} 0 & 1 & -2 \\ 4 & 4 & 4 \\ 2 & 9 & 0 \end{pmatrix}$

We are given that $b_{ij}$ is the cofactor of $a_{ij}$ in matrix A. We are asked to find the value of $\sqrt[3]{\det(d_{ij})}$, where $d_{ij} = \sum_{k=1}^{3} a_{ik}b_{jk}$.

Let D be the matrix with elements $d_{ij}$. The expression $d_{ij} = \sum_{k=1}^{3} a_{ik}b_{jk}$ is the element in the $i$-th row and $j$-th column of the matrix product $A (\text{adj}(A))^T$, where $\text{adj}(A)$ is the adjugate matrix of A. The elements of $\text{adj}(A)$ are $(\text{adj}(A))_{ij} = b_{ji}$. So, the elements of $(\text{adj}(A))^T$ are $((\text{adj}(A))^T)_{ij} = (\text{adj}(A))_{ji} = b_{ij}$. Thus, $d_{ij} = \sum_{k=1}^{3} a_{ik} ((\text{adj}(A))^T)_{kj} = \sum_{k=1}^{3} a_{ik} b_{jk}$.

Alternatively, we know the property that for a matrix A and its cofactors $b_{ij}$, $\sum_{k=1}^{n} a_{ik} b_{jk} = \det(A) \delta_{ij}$, where $\delta_{ij}$ is the Kronecker delta ($\delta_{ij}=1$ if $i=j$ and $\delta_{ij}=0$ if $i \neq j$). So, $d_{ij} = \det(A) \delta_{ij}$.

This means the matrix D is a diagonal matrix: $D = \begin{pmatrix} \det(A) & 0 & 0 \\ 0 & \det(A) & 0 \\ 0 & 0 & \det(A) \end{pmatrix} = \det(A) I$, where I is the $3 \times 3$ identity matrix.

The determinant of D is $\det(D) = \det(\det(A) I)$. For a scalar $c$ and an $n \times n$ matrix M, $\det(cM) = c^n \det(M)$. Here, $c = \det(A)$, $M = I$, and $n=3$. So, $\det(D) = (\det(A))^3 \det(I) = (\det(A))^3 \times 1 = (\det(A))^3$.

The value we need to find is $\sqrt[3]{\det(d_{ij})} = \sqrt[3]{\det(D)} = \sqrt[3]{(\det(A))^3}$. Since $\det(A)$ is a real number for a real matrix A, $\sqrt[3]{(\det(A))^3} = \det(A)$.

Now, we need to calculate the determinant of matrix A. $A = \begin{pmatrix} 0 & 1 & -2 \\ 4 & 4 & 4 \\ 2 & 9 & 0 \end{pmatrix}$

We can calculate $\det(A)$ by expanding along the first row: $\det(A) = 0 \cdot \det \begin{pmatrix} 4 & 4 \\ 9 & 0 \end{pmatrix} - 1 \cdot \det \begin{pmatrix} 4 & 4 \\ 2 & 0 \end{pmatrix} + (-2) \cdot \det \begin{pmatrix} 4 & 4 \\ 2 & 9 \end{pmatrix}$ $\det(A) = 0 - 1 \cdot (4 \times 0 - 4 \times 2) - 2 \cdot (4 \times 9 - 4 \times 2)$ $\det(A) = -1 \cdot (0 - 8) - 2 \cdot (36 - 8)$ $\det(A) = -1 \cdot (-8) - 2 \cdot (28)$ $\det(A) = 8 - 56$ $\det(A) = -48$.

Alternatively, we can factor out 4 from the second row of A: $\det(A) = 4 \det \begin{pmatrix} 0 & 1 & -2 \\ 1 & 1 & 1 \\ 2 & 9 & 0 \end{pmatrix}$ Now, expand the new determinant along the first row: $0 \cdot \det \begin{pmatrix} 1 & 1 \\ 9 & 0 \end{pmatrix} - 1 \cdot \det \begin{pmatrix} 1 & 1 \\ 2 & 0 \end{pmatrix} + (-2) \cdot \det \begin{pmatrix} 1 & 1 \\ 2 & 9 \end{pmatrix}$ $= 0 - 1 \cdot (1 \times 0 - 1 \times 2) - 2 \cdot (1 \times 9 - 1 \times 2)$ $= -1 \cdot (-2) - 2 \cdot (9 - 2)$ $= 2 - 2 \cdot (7)$ $= 2 - 14 = -12$. So, $\det(A) = 4 \times (-12) = -48$.

The determinant of A is -48. The value we need to find is $\det(A)$, which is -48.

Comparing with the given options: (A) 4 (B) 24 (C) -48 (D) -24

The value is -48, which matches option (C).

The final answer is $\boxed{-48}$.

Explanation of the solution:

1. Construct the matrix A based on the given conditions for its elements $a_{ij}$.
2. Recognize that the elements $d_{ij} = \sum_{k=1}^{3} a_{ik}b_{jk}$ (where $b_{jk}$ is the cofactor of $a_{jk}$) form a matrix D which is equal to $\det(A) I$, where I is the identity matrix. This is a property of determinants and cofactors: $\sum_{k=1}^{n} a_{ik} b_{jk} = \det(A) \delta_{ij}$.
3. Calculate the determinant of D. Since $D = \det(A) I$, $\det(D) = (\det(A))^3$.
4. The required value is $\sqrt[3]{\det(D)} = \sqrt[3]{(\det(A))^3} = \det(A)$.
5. Calculate the determinant of the matrix A.
6. The calculated determinant of A is the final answer.

Matrix A: $A = \begin{pmatrix} 0 & 1 & -2 \\ 4 & 4 & 4 \\ 2 & 9 & 0 \end{pmatrix}$ $\det(A) = 0(0-36) - 1(0-8) - 2(36-8) = 0 + 8 - 2(28) = 8 - 56 = -48$. The value is $\det(A) = -48$.

The final answer is $\boxed{-48}$.