Question

Consider a long glass slab of width of 50 cm and is placed in first quadrant shown a ray just parallel to y-axis enters the medium. The refractive index of medium varies according to law $\mu = \frac{1}{1-x}$ then choose correct statement's

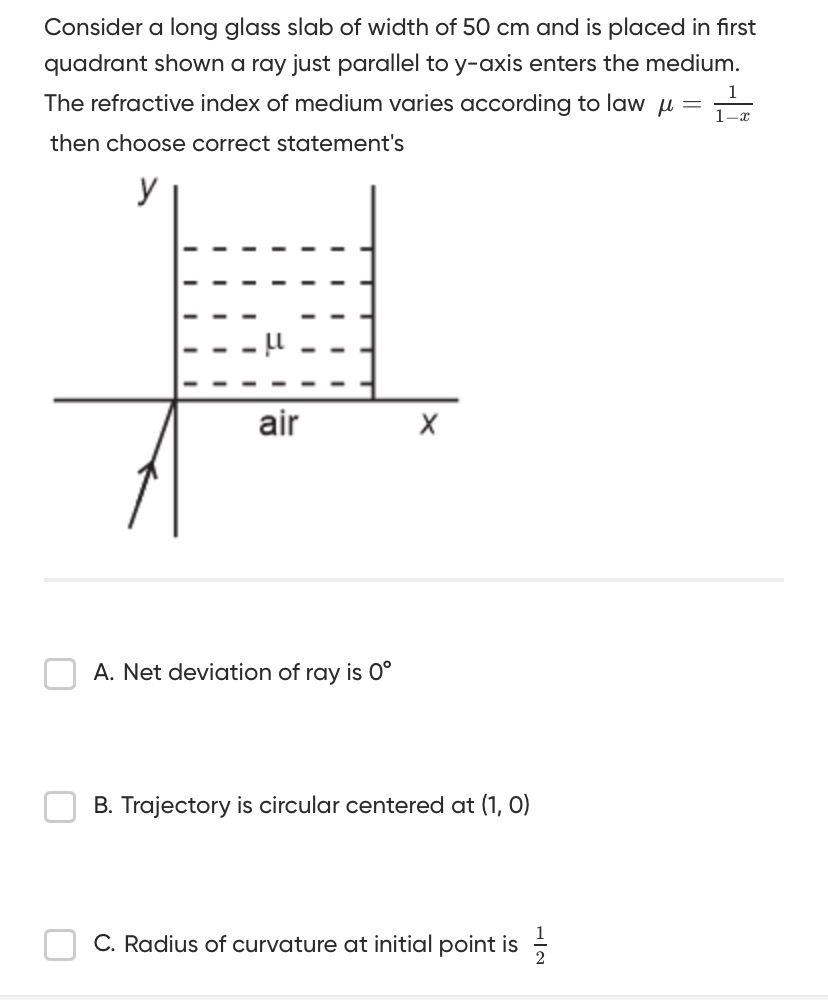
• A. Net deviation of ray is 0°
• B. Trajectory is circular centered at (1, 0)
• C. Radius of curvature at initial point is $\frac{1}{2}$

Answer 1

Answer: (A), (B)

A, B

Answer 2

The problem describes a light ray entering a medium with a spatially varying refractive index. We need to determine the trajectory of the ray and its deviation.

1. Initial Conditions and Refraction at Entry (x=0):

The ray enters the medium at $x=0$, parallel to the y-axis. The refractive index of air is $\mu_{air} = 1$. The refractive index of the medium at $x=0$ is $\mu(0) = \frac{1}{1-0} = 1$. The normal to the interface (x=0) is along the x-axis. Since the incident ray is parallel to the y-axis, the angle of incidence with the normal is $i = 90^\circ$. Applying Snell's Law at the interface: $\mu_{air} \sin i = \mu(0) \sin r$ $1 \cdot \sin(90^\circ) = 1 \cdot \sin r$ $1 = \sin r \implies r = 90^\circ$. This means the ray enters the medium without changing its direction; it continues to propagate parallel to the y-axis inside the medium at $x=0$.

2. Ray Path in the Medium (Gradient Index Optics):

For a medium where the refractive index varies only with $x$ (i.e., $\mu = \mu(x)$), the quantity $\mu \sin \alpha$ is conserved, where $\alpha$ is the angle the ray makes with the x-axis (the direction of refractive index variation). At the entry point $(x=0)$, the ray is parallel to the y-axis. Therefore, the angle it makes with the x-axis is $\alpha_0 = 90^\circ$. The value of the conserved quantity is $\mu(0) \sin \alpha_0 = 1 \cdot \sin(90^\circ) = 1$. So, for any point $(x,y)$ on the ray's path: $\mu(x) \sin \alpha = 1$ Substituting $\mu(x) = \frac{1}{1-x}$: $\frac{1}{1-x} \sin \alpha = 1 \implies \sin \alpha = 1-x$

The slope of the ray is $\frac{dy}{dx} = \tan \alpha = \frac{\sin \alpha}{\cos \alpha} = \frac{\sin \alpha}{\sqrt{1-\sin^2 \alpha}}$. Substituting $\sin \alpha = 1-x$: $\frac{dy}{dx} = \frac{1-x}{\sqrt{1-(1-x)^2}}$ To find the trajectory, we integrate this differential equation: $dy = \frac{1-x}{\sqrt{1-(1-x)^2}} dx$ Let $u = 1-x$, so $du = -dx$. $dy = \frac{u}{\sqrt{1-u^2}} (-du) = -\frac{u}{\sqrt{1-u^2}} du$ Integrating both sides: $\int dy = -\int \frac{u}{\sqrt{1-u^2}} du$ Let $v = 1-u^2$, then $dv = -2u du$, so $u du = -\frac{1}{2} dv$. $y = -\int \frac{-\frac{1}{2} dv}{\sqrt{v}} = \frac{1}{2} \int v^{-1/2} dv = \frac{1}{2} \frac{v^{1/2}}{1/2} + C = \sqrt{v} + C$ Substitute back $v = 1-u^2$ and $u = 1-x$: $y = \sqrt{1-(1-x)^2} + C$ The ray enters at the origin $(0,0)$. So, substitute $x=0, y=0$: $0 = \sqrt{1-(1-0)^2} + C \implies 0 = \sqrt{1-1} + C \implies 0 = 0 + C \implies C=0$. Thus, the equation of the trajectory is $y = \sqrt{1-(1-x)^2}$. Squaring both sides: $y^2 = 1-(1-x)^2$ Rearranging: $(1-x)^2 + y^2 = 1$ or $(x-1)^2 + y^2 = 1$. This is the equation of a circle centered at $(1,0)$ with a radius of $R=1$.

3. Evaluate the Statements:

• B. Trajectory is circular centered at (1, 0) As derived, the trajectory is $(x-1)^2 + y^2 = 1$, which is a circle centered at $(1,0)$. This statement is correct.

• C. Radius of curvature at initial point is $\frac{1}{2}$ Since the trajectory is a circle with radius $R=1$, the radius of curvature at any point on the circle (including the initial point) is constant and equal to the radius, which is 1. This statement is incorrect.

• A. Net deviation of ray is 0° The slab has a width of 50 cm, meaning it extends from $x=0$ to $x=0.5$ m (assuming consistent units with the equation of trajectory where the center is at $x=1$). The ray enters at $x=0$. It exits the slab at $x=0.5$. At the exit point ($x=0.5$), the angle $\alpha$ the ray makes with the x-axis is given by: $\sin \alpha = 1-x = 1-0.5 = 0.5$ So, $\alpha = 30^\circ$. This angle $\alpha$ is the angle of incidence ($i_{exit}$) at the exit surface, because the normal to the exit surface (at $x=0.5$) is parallel to the x-axis. The refractive index of the medium at the exit surface is $\mu(0.5) = \frac{1}{1-0.5} = \frac{1}{0.5} = 2$. Applying Snell's Law at the exit interface: $\mu(0.5) \sin i_{exit} = \mu_{air} \sin r_{exit}$ $2 \cdot \sin(30^\circ) = 1 \cdot \sin r_{exit}$ $2 \cdot \frac{1}{2} = \sin r_{exit}$ $1 = \sin r_{exit} \implies r_{exit} = 90^\circ$. This means the ray exits the slab making an angle of $90^\circ$ with the x-axis, i.e., it exits parallel to the y-axis. Since the ray entered parallel to the y-axis and exits parallel to the y-axis, the net deviation of the ray is $0^\circ$. This statement is correct.

Conclusion: Statements A and B are correct.