Question

Consider a Line L having $eq^n (\overrightarrow{r}-\overrightarrow{p})\times\overrightarrow{a}=\overrightarrow{0}$ and plane having $eq^n \overrightarrow{r}=\overrightarrow{g}+\lambda\overrightarrow{b}+\mu\overrightarrow{c}$

If $\overrightarrow{a}\times(\overrightarrow{b}\times\overrightarrow{c})\neq0$ and $[\overrightarrow{a}\overrightarrow{b}\overrightarrow{c}]=0$ then

Comment on Plane & Line

Answer 1

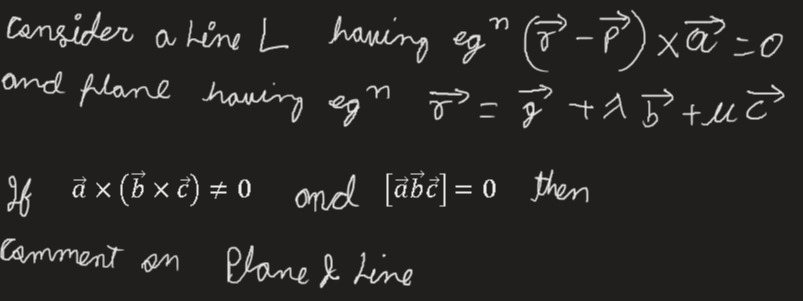
The line L is parallel to the plane P.

Answer 2

To comment on the relationship between the line L and the plane P, we first analyze their given equations and the provided conditions.

1. Understanding the Line L: The equation of the line L is given by $(\overrightarrow{r}-\overrightarrow{p})\times\overrightarrow{a}=\overrightarrow{0}$. This implies that the vector $(\overrightarrow{r}-\overrightarrow{p})$ is parallel to $\overrightarrow{a}$. Thus, the line L passes through the point with position vector $\overrightarrow{p}$ and has a direction vector $\overrightarrow{d_L} = \overrightarrow{a}$.

2. Understanding the Plane P: The equation of the plane P is given by $\overrightarrow{r}=\overrightarrow{g}+\lambda\overrightarrow{b}+\mu\overrightarrow{c}$. This is the vector equation of a plane passing through the point with position vector $\overrightarrow{g}$ and parallel to the vectors $\overrightarrow{b}$ and $\overrightarrow{c}$. The normal vector to the plane P, $\overrightarrow{n_P}$, is given by the cross product of its parallel vectors: $\overrightarrow{n_P} = \overrightarrow{b}\times\overrightarrow{c}$. For $\overrightarrow{b}$ and $\overrightarrow{c}$ to define a plane, they must be non-collinear, which means $\overrightarrow{b}\times\overrightarrow{c} \neq \overrightarrow{0}$.

3. Analyzing the Conditions:

• Condition 1: $\overrightarrow{a}\times(\overrightarrow{b}\times\overrightarrow{c})\neq\overrightarrow{0}$

  Let $\overrightarrow{N} = \overrightarrow{b}\times\overrightarrow{c}$ be the normal vector to the plane. This condition becomes $\overrightarrow{a}\times\overrightarrow{N}\neq\overrightarrow{0}$. This implies that the direction vector of the line, $\overrightarrow{a}$, is not parallel to the normal vector of the plane, $\overrightarrow{N}$. If a line's direction vector is parallel to a plane's normal vector, the line is perpendicular to the plane. Since $\overrightarrow{a}$ is not parallel to $\overrightarrow{N}$, the line L is not perpendicular to the plane P.

• Condition 2: $[\overrightarrow{a}\overrightarrow{b}\overrightarrow{c}]=0$

  The scalar triple product $[\overrightarrow{a}\overrightarrow{b}\overrightarrow{c}]$ is defined as $\overrightarrow{a}\cdot(\overrightarrow{b}\times\overrightarrow{c})$. So, this condition means $\overrightarrow{a}\cdot(\overrightarrow{b}\times\overrightarrow{c})=0$. Substituting $\overrightarrow{N} = \overrightarrow{b}\times\overrightarrow{c}$, we get $\overrightarrow{a}\cdot\overrightarrow{N}=0$. This implies that the direction vector of the line, $\overrightarrow{a}$, is perpendicular to the normal vector of the plane, $\overrightarrow{N}$.

4. Combining the Conditions: If the direction vector of a line is perpendicular to the normal vector of a plane, then the line is parallel to the plane. So, from Condition 2, we conclude that the line L is parallel to the plane P.

Now let's consider Condition 1 again in light of this conclusion. We have $\overrightarrow{a} \cdot \overrightarrow{N} = 0$ (from Condition 2). We also know that $\overrightarrow{a}$ is a direction vector, so $\overrightarrow{a} \neq \overrightarrow{0}$. And $\overrightarrow{N} = \overrightarrow{b}\times\overrightarrow{c}$ is the normal vector of a plane, so $\overrightarrow{N} \neq \overrightarrow{0}$. If two non-zero vectors are perpendicular, they cannot be parallel. Therefore, if $\overrightarrow{a} \cdot \overrightarrow{N} = 0$, then it must be true that $\overrightarrow{a} \times \overrightarrow{N} \neq \overrightarrow{0}$ (unless one of them is a zero vector, which is not the case here). Thus, Condition 1 ($\overrightarrow{a}\times(\overrightarrow{b}\times\overrightarrow{c})\neq\overrightarrow{0}$) is consistent with and, in fact, implied by Condition 2, given that $\overrightarrow{a}$ and $\overrightarrow{b}\times\overrightarrow{c}$ are non-zero vectors.

Conclusion: The primary conclusion from the given conditions is that the line L is parallel to the plane P. We cannot determine if the line lies within the plane or is strictly parallel to it, as that would require checking if a point on the line (e.g., $\overrightarrow{p}$) satisfies the plane's equation, i.e., $(\overrightarrow{p}-\overrightarrow{g})\cdot(\overrightarrow{b}\times\overrightarrow{c})=0$. This information is not provided.

The final answer is $\boxed{Line \ is \ parallel \ to \ the \ plane}$

Explanation of the solution:

The line L has direction vector $\overrightarrow{a}$. The plane P has normal vector $\overrightarrow{n_P} = \overrightarrow{b}\times\overrightarrow{c}$. The condition $[\overrightarrow{a}\overrightarrow{b}\overrightarrow{c}]=0$ means $\overrightarrow{a}\cdot(\overrightarrow{b}\times\overrightarrow{c})=0$, which implies $\overrightarrow{a}\cdot\overrightarrow{n_P}=0$. This signifies that the direction vector of the line is perpendicular to the normal vector of the plane. Therefore, the line is parallel to the plane. The condition $\overrightarrow{a}\times(\overrightarrow{b}\times\overrightarrow{c})\neq\overrightarrow{0}$ means $\overrightarrow{a}\times\overrightarrow{n_P}\neq\overrightarrow{0}$, which implies $\overrightarrow{a}$ is not parallel to $\overrightarrow{n_P}$. This is consistent with $\overrightarrow{a}\cdot\overrightarrow{n_P}=0$ for non-zero vectors $\overrightarrow{a}$ and $\overrightarrow{n_P}$. Thus, the line is parallel to the plane.