Question
Question: Consider a ladder network shown in figure. What should be the value off resistance R, so that effect...
Consider a ladder network shown in figure. What should be the value off resistance R, so that effective resistance between A and B becomes independent of the number of elements in the combination?
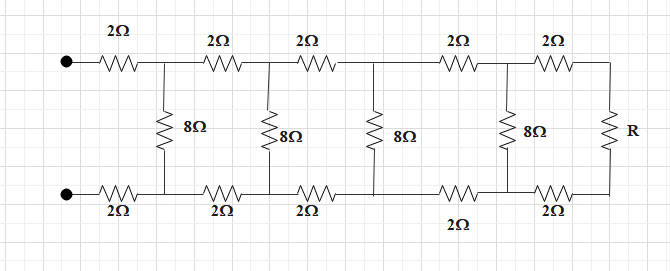
A. 2ΩB. 4ΩC. 8ΩD. 16Ω
Solution
Obtain the expression for the total resistance of a circuit when we connect more than one resistance in series and in parallel. Observe the circuit given where we have the same resistances in every loop of the circuit and every 8Ω resistance is connected in parallel to the previous loop. When we consider, every 8Ω resistance is connected in parallel to the total 8Ω resistance of the loop, then the total resistance is independent of the number of elements in the circuit.
Complete answer:
If we observe the circuit carefully, in every loop of the ladder network, we have two 2Ω resistance connected in series with another resistance.
Now, we need to select the resistance R such that the total effective resistance between A and B will be independent of the number of elements in the combination. To do this we need to make the resistance connected in series with the two 2Ω resistance in every loop equal.
When two resistances R1 and R2 are connected in series in a circuit, the total resistance of the circuit is given as,
R=R1+R2
When two resistances R1 and R2 are connected in parallel to each other in a circuit, the total resistance of the circuit is given as,
R1=R11+R21
Now, if we observe the above combination, the resistance of each branch is 8Ω . if we consider two 2Ω and one 4Ω resistance connected in series, then the total resistance will be 8Ω. When two 8Ω are connected in parallel, the total resistance will become 4Ω. This total 4Ω resistance will be again connected in series with the previous two 2Ω resistances to give a 8Ω resistance. This way at the end we will always get a total of 8Ω resistance which will be independent of the number of elements in the combination.
For this to happen at the last loop we need to get a 8Ω resistance in parallel connection with the 8Ω resistance of the previous loop. At the last branch we have two 2Ω resistances connected in series with another resistance R.
We can write,
