Question
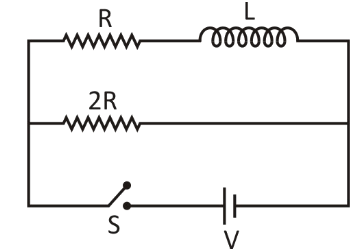
Question: Consider a \[L - R\] circuit as shown in the figure. There is no current in the circuit. Switch \[S\...
Consider a L−R circuit as shown in the figure. There is no current in the circuit. Switch S is closed at t=0 , time instant when current in inductor is equal to current in resistor 2R will be:
(1) RLln2
(2) R2Lln2
(3) 2RLln2
(4) 2RL
Solution
First of all, we will find the current at any instant which involves time constant. The current initially is given by the resistance R and the current at any instant is given by the resistance 2R . We will substitute the required values and manipulate accordingly and obtain the result.
Complete Step by step answer: In the given question, we are given a L−R circuit.
There is present no current in the circuit.
At time t=0, the switch is closed.
We are asked to find out the time instant when the current in the inductor is equal to the current in the resistor 2R .
To begin with, we will have to find the current in the current at any given instant, which can be easily found by the use of equation. We know the time constant which is represented by a Greek letter tau, which is the ratio of inductance and resistance. We will find the current flowing through the resistor R according to Ohm’s law, which is the current flowing initially.
So, let us find the find, at any instant, which is given by the equation:
i=i01−eτ−t …… (1)
Where,
i indicates the current at any instant.
i0 indicates the current initially.
t indicates the time.
τ indicates the time constant.
The time constant is the ratio of inductance and resistance, which can be written as:
τ=RL
Where,
L indicates inductance.
R indicates resistance.
Again, we can write, the current in the resistor R , which is given by Ohm’s law as:
i0=RV …… (2)
We can write:
i=i2R
And,
i2R=2RV
Now, we can modify the equation (1), as:
i=i01−eτ−t ⇒i2R=i01−eτ−t ⇒2RV=RV1−eτ−t ⇒21=1−eτ−t
Again, we manipulate further,
⇒eτ−t=1−21 ⇒eτ−t=21 ⇒ln2=τt
We further simplify,
⇒t=τln2 ⇒t=RLln2
Hence, the time instant when the current in the inductor is equal to the current in the resistor 2R is RLln2.
The correct option is (1).
Note: In this circuit, there are combinations of resistances and inductors. In an AC circuit, the inductor present helps to reduce the voltage, without any significant loss in energy. In practical AC circuits, the power factor ranges between 0 to 1 again depending on the passive components which are present within the load connected.
