Question
Question: Consider a function $f(x)=\int sin(ln \ x)dx$ such that $f(e)=\frac{e}{\sqrt{2}}sin(1-\frac{\pi}{4})...
Consider a function f(x)=∫sin(ln x)dx such that f(e)=2esin(1−4π). Then the value of f(1) is
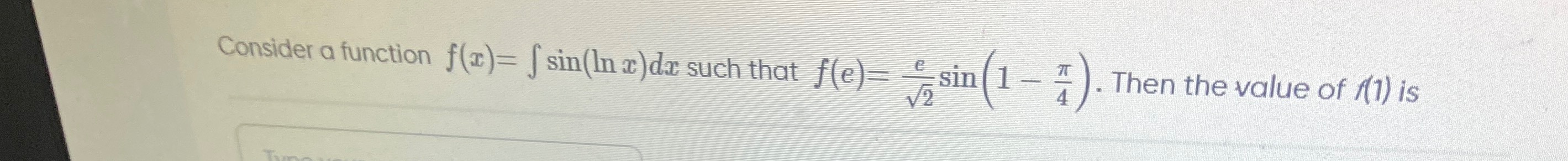
21
−21
1
−1
-\frac{1}{2}
Solution
To find the value of f(1), we first need to evaluate the indefinite integral f(x)=∫sin(lnx)dx.
Step 1: Evaluate the indefinite integral f(x)=∫sin(lnx)dx.
Let I=∫sin(lnx)dx. We can use the substitution method. Let t=lnx. Then x=et, and differentiating both sides with respect to t, we get dx=etdt. Substituting these into the integral: I=∫sin(t)etdt.
This is a standard integral of the form ∫eaxsin(bx)dx=a2+b2eax(asin(bx)−bcos(bx)). In our case, a=1 and b=1. So, I=12+12et(1⋅sin(t)−1⋅cos(t))+C′ I=2et(sin(t)−cos(t))+C′.
Now, substitute back t=lnx and et=x: f(x)=2x(sin(lnx)−cos(lnx))+C.
Step 2: Use the given condition f(e)=2esin(1−4π) to find the constant C.
Substitute x=e into the expression for f(x): f(e)=2e(sin(lne)−cos(lne))+C. Since lne=1: f(e)=2e(sin(1)−cos(1))+C.
Now, let's simplify the given value of f(e): f(e)=2esin(1−4π). Using the trigonometric identity sin(A−B)=sinAcosB−cosAsinB: sin(1−4π)=sin(1)cos(4π)−cos(1)sin(4π). We know that cos(4π)=21 and sin(4π)=21. So, sin(1−4π)=sin(1)21−cos(1)21=21(sin(1)−cos(1)).
Substitute this back into the expression for f(e): f(e)=2e⋅21(sin(1)−cos(1)) f(e)=2e(sin(1)−cos(1)).
Now, equate the two expressions for f(e): 2e(sin(1)−cos(1))+C=2e(sin(1)−cos(1)). From this equation, it is clear that C=0.
So, the definite form of the function is: f(x)=2x(sin(lnx)−cos(lnx)).
Step 3: Calculate the value of f(1).
Substitute x=1 into the function f(x): f(1)=21(sin(ln1)−cos(ln1)). We know that ln1=0. So, f(1)=21(sin(0)−cos(0)). We know that sin(0)=0 and cos(0)=1. f(1)=21(0−1) f(1)=−21.
The final answer is −21.
Explanation of the solution:
-
Integrate f(x): The integral ∫sin(lnx)dx is solved by substitution t=lnx, transforming it into ∫etsintdt. This is a standard integral form ∫eaxsin(bx)dx=a2+b2eax(asin(bx)−bcos(bx)). Applying this formula with a=1,b=1 and then substituting back t=lnx yields f(x)=2x(sin(lnx)−cos(lnx))+C.
-
Determine Constant C: Use the given condition f(e)=2esin(1−4π). Substitute x=e into f(x) to get f(e)=2e(sin(1)−cos(1))+C. Simplify the given f(e) using the trigonometric identity sin(A−B)=sinAcosB−cosAsinB, which gives 2esin(1−4π)=2e(sin(1)−cos(1)). Equating the two expressions for f(e) reveals C=0.
-
Calculate f(1): With C=0, f(x)=2x(sin(lnx)−cos(lnx)). Substitute x=1 into this function. Since ln1=0, f(1)=21(sin(0)−cos(0)). Using sin(0)=0 and cos(0)=1, we get f(1)=21(0−1)=−21.
