Question

Consider a function $f(x)= \int \frac{(2x^2-1)}{(1-x^2+x^4)^{\frac{1}{4}}} dx, x>0$, $f(1)= \frac{2}{3}$. If $f(\frac{1}{\sqrt{2}})= \frac{2}{3}k^k$, then the value of $k$ is

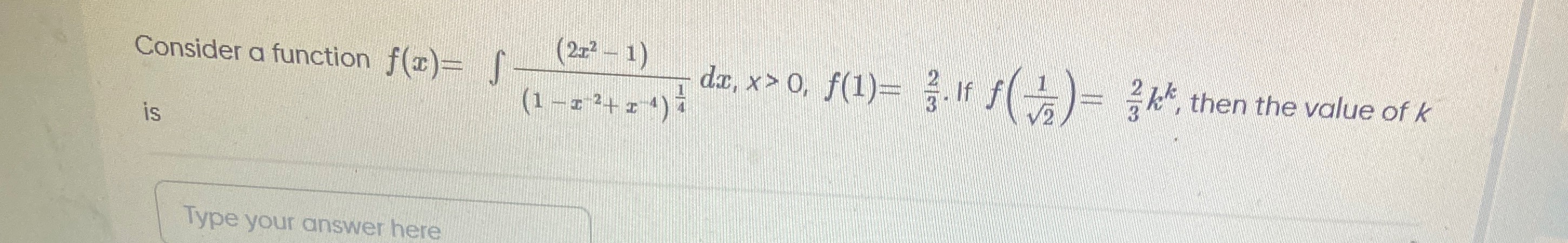
Answer 1

Not provided

Answer 2

The provided solution attempts to solve the integral but does not arrive at a final answer. Therefore, an explanation and correct answer cannot be derived from the given information.