Question
Question: Consider a finite line charge of uniform charge density \(\lambda \) and of length L lying along the...
Consider a finite line charge of uniform charge density λ and of length L lying along the x-axis from to x=0. find the field at a point along the axis at x=d.
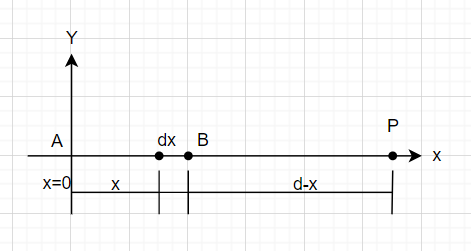
Solution
First of all, we will consider an element dx and then calculate the Electric field about that dx element. After that, we will do integration of the resulting electric field expression that we found with the help of the dx element. So, as to get the Electric field expression at that particular given point which is point P.
Formula Used: Here, expression for Electric Field is :-E=4πεo1⋅r2q
Where, E is the electric field that occurs due to charge ’q’ ,εo is the permittivity of free space.
Complete step-by-step solution:
Since,dE=4πεo1⋅(d−x)2dq
Now, dxdq=λ
So, ⇒dq=λdx
therefore,⇒dE=4πεo1⋅(d−x)2λdx
After integrating both sides. We get,
⇒∫0vdE=∫0L[4πεo1⋅(d−x)2λdx]
Taking constants out of integration,
⇒E=4πεoλ∫0L[(d−x)2dx]
⇒E=4πεoλ[d−x1]0L
After putting limits,⇒E=4πεoλ[(d−L)1−d1]
Then after Multiplying it, we get :-
⇒E=4πεoλ[d(d−L)−d+(d−L)]
⇒E=4πεoλ[d(d−L)L]
Electric field,⇒E=4πεo⋅d(d−L)λL
Hence, the Electric field at a point P along the axis at x=d. Having uniform charge density as well as length L lying along the x-axis from x=0 to that point is E=4πεo⋅d(d−L)λL
Additional Information: Electric field is an electric property connected with each point in space only when an electric charge is present in any form. The magnitude and direction of the electric field are expressed by the value of E and are called electric field strength or electric field intensity or you can simply call it the electric field. We can get Knowledge of the value of the electric field at a point, without having any specific knowledge of what produced the field, all that we need is to determine what will happen to electric charges close or present nearer to that particular point.
Note: Firstly, we have to find the electric field for element dx. Then only, through the integration of the elemental electric field, will we be able to get the resultant electric field for the given point. Also, try to prefer solving equations in a stepwise manner. If, doesn't want to stick anywhere and do the integration as well, put the limits carefully.
