Question

Consider a differential equation $f'(\tan x)=\frac{\tan x}{f(\tan x)} + \frac{f(\tan x)}{\tan x}, f(1)=\sqrt{3}$

Then the value of $(f(\sqrt{3}))^2 - 3\ln 3$ is

Answer 1

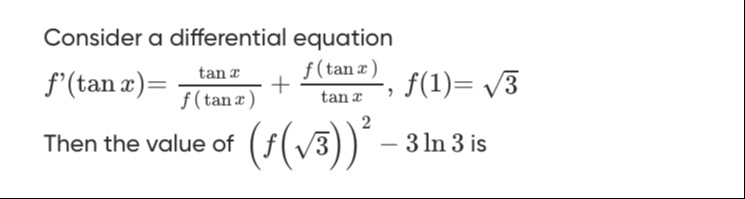
9

Answer 2

Let $t = \tan x$. The given differential equation is $f'(t) = \frac{t}{f(t)} + \frac{f(t)}{t}$. We can rewrite this as $\frac{df}{dt} = \frac{t}{f(t)} + \frac{f(t)}{t}$.

Using the substitution $f(t) = t g(t)$, we have $f'(t) = g(t) + t g'(t)$. Substituting into the differential equation: $g(t) + t g'(t) = \frac{t}{t g(t)} + \frac{t g(t)}{t}$ $g(t) + t g'(t) = \frac{1}{g(t)} + g(t)$ $t g'(t) = \frac{1}{g(t)}$

This is a separable differential equation: $g(t) \frac{dg}{dt} = \frac{1}{t}$ $g \, dg = \frac{1}{t} \, dt$

Integrating both sides: $\int g \, dg = \int \frac{1}{t} \, dt$ $\frac{g(t)^2}{2} = \ln|t| + C$ $g(t)^2 = 2 \ln|t| + K$, where $K = 2C$.

Substituting back $g(t) = \frac{f(t)}{t}$: $\left(\frac{f(t)}{t}\right)^2 = 2 \ln|t| + K$ $\frac{f(t)^2}{t^2} = 2 \ln|t| + K$ $f(t)^2 = t^2 (2 \ln|t| + K)$

Using the initial condition $f(1) = \sqrt{3}$: $f(1)^2 = (1)^2 (2 \ln|1| + K)$ $(\sqrt{3})^2 = 1 (2 \cdot 0 + K)$ $3 = K$

So, the equation for $f(t)^2$ becomes: $f(t)^2 = t^2 (2 \ln|t| + 3)$

To find $(f(\sqrt{3}))^2$, substitute $t = \sqrt{3}$: $(f(\sqrt{3}))^2 = (\sqrt{3})^2 (2 \ln|\sqrt{3}| + 3)$ $(f(\sqrt{3}))^2 = 3 (2 \ln(\sqrt{3}) + 3)$ $(f(\sqrt{3}))^2 = 3 (2 \cdot \frac{1}{2} \ln 3 + 3)$ $(f(\sqrt{3}))^2 = 3 (\ln 3 + 3)$ $(f(\sqrt{3}))^2 = 3 \ln 3 + 9$

Finally, calculate the required expression: $(f(\sqrt{3}))^2 - 3\ln 3 = (3 \ln 3 + 9) - 3\ln 3 = 9$.