Question

Consider a cylinder of mass $M$ resting on a rough horizontal rug that is pulled out from under it with acceleration $a$ perpendicular to the axis of the cylinder. What is ${F_{friction}}$ at the point P? It is assumed that the cylinder does not slip.

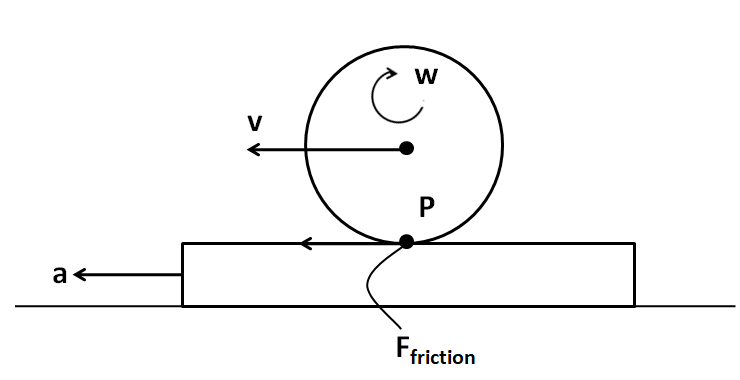
(A) $Mg$
(B) $Ma$
(C) $\dfrac{{Ma}}{2}$
(D) $\dfrac{{Ma}}{3}$

Answer 1

To solve this question, we need to consider the free body diagram of the cylinder. Then, applying the Newton’s second law on the linear and the rotational motion of the cylinder, we will get the final answer.
Formula Used: The formulae used in solving this question are given by
$\Rightarrow \tau = I\alpha$ , here $\tau$ is the torque applied, $\alpha$ is the angular acceleration, and $I$ is the moment of inertia.
$\Rightarrow I = \dfrac{{M{R^2}}}{2}$ , here $I$ is the moment of inertia of a solid cylinder of mass $M$ and radius $R$ about the axis passing through its centre of gravity and perpendicular to the circular cross section.

Complete step by step answer:
Let the acceleration of the centre of mass of the cylinder be ${a_{com}}$ and the angular acceleration of the cylinder be $\alpha$
Making the free body diagram of the cylinder, we have

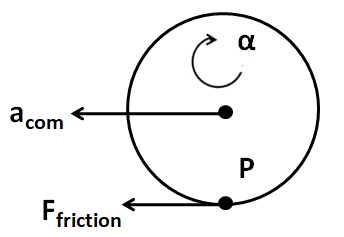
As the only force acting on the wheel is the force of friction, so from the Newton’s second law we have
$\Rightarrow {F_{friction}} = M{a_{com}}$ ………………..(1)
Now, we consider the acceleration of the point P. We see that it has two components. One due to the acceleration of the centre of mass $\left( {{a_{com}}} \right)$ , and the other one due to the angular acceleration of the cylinder $\left( {\alpha R} \right)$ . As both these are in the same direction, so the total acceleration of P becomes
$\Rightarrow {a_P} = {a_{com}} + \alpha R$
Since the cylinder does not slip on the horizontal rug, so the acceleration of the rug and the cylinder at the point of contact P are equal. That is, that acceleration of the point P of the cylinder is equal to $a$ towards the left.
$\Rightarrow {a_P} = a$ ………………..(2)
From (1) and (2), we have
$\Rightarrow a = {a_{com}} + \alpha R$ ………………..(3)
Now, the angular acceleration of the cylinder is due to the torque applied by the force of friction, which is given by
$\Rightarrow \tau = {F_{friction}}R$ ………………..(4)
We know that the torque is related to the angular acceleration by
$\Rightarrow \tau = I\alpha$ ………………..(5)
From (4) and (5)
$\Rightarrow I\alpha = {F_{friction}}R$ ………………..(6)
The moment of inertia of the cylinder about the given axis of rotation is
$\Rightarrow I = \dfrac{{M{R^2}}}{2}$
Substituting this in (6)
$\Rightarrow \dfrac{{M{R^2}}}{2}\alpha = {F_{friction}}R$
$\Rightarrow \alpha = \dfrac{{{F_{friction}}R}}{{\dfrac{{M{R^2}}}{2}}}$
So we get the angular acceleration as
$\Rightarrow \alpha = \dfrac{{2{F_{friction}}}}{{MR}}$
Substituting this in (3) we have
$\Rightarrow a = {a_{com}} + \left( {\dfrac{{2{F_{friction}}}}{{MR}}} \right)R$
$\Rightarrow a = {a_{com}} + \dfrac{{2{F_{friction}}}}{M}$
So we get the acceleration of the center of mass as
$\Rightarrow {a_{com}} = a - \dfrac{{2{F_{friction}}}}{M}$
Finally substituting this in (1), we get
$\Rightarrow {F_{friction}} = M\left( {a - \dfrac{{2{F_{friction}}}}{M}} \right)$
$\Rightarrow {F_{friction}} = \dfrac{{Ma}}{3}$
Thus the force of friction at the point P is equal to $\dfrac{{Ma}}{3}$ .
Hence, the correct answer is option D.

Note:
This question can also be attempted with the horizontal rug as the frame of reference. As it is an accelerating frame, we will need to apply a pseudo force equal to $Ma$ , in the direction opposite to the acceleration of the horizontal rug. Also, the acceleration of the point P of the cylinder will be zero in that frame.