Question

Consider a curve $a{{x}^{2}}+2hxy+b{{y}^{2}}=1$ and point P not on the curve. A line is drawn from the point P intersect the curve at points Q & R. If the product PQ.PR is independent of the slope of the line, then show that the curve is a circle.

Answer 1

This question belongs to the topic of geometry. In this question, first we will take reference from the figure for understanding the question carefully. After that, we will find the equation of line using point P and the angle of inclination. After that, we will take the value of x and y from the equation of line and put them in the equation of the curve. After that, we will solve the equation and find the conditions where PQ.PR is independent of slope. After doing further solution, we will prove which is asked to prove.

Complete step by step answer:
Let us solve this question.
The question says that a curve $a{{x}^{2}}+2hxy+b{{y}^{2}}=1$ is given and there is a point P near the curve but not on the curve. There are two points Q and R on the curve. We have to prove that the curve is a circle if the product PQ.PR is independent of slope of line. We can take reference from the following figure.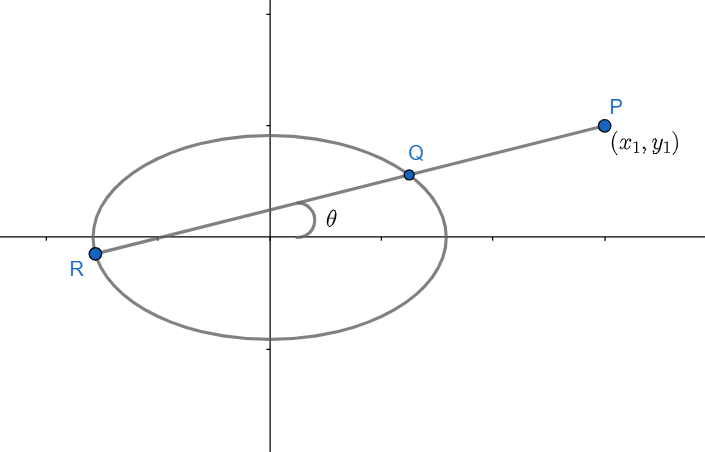
As point P is $\left( {{x}_{1}},{{y}_{1}} \right)$. Let $\theta$ be the angle of inclination of line PR which is passing through point P, Q, and R. The equation of this line will be
$\dfrac{y-{{y}_{1}}}{\sin \theta }=\dfrac{x-{{x}_{1}}}{\cos \theta }=r$
Here, r is the distance of line from point P to the point somewhere at the line.
We can write the above equation as
$y={{y}_{1}}+r\sin \theta$ and $x={{x}_{1}}+r\cos \theta$
As points Q and R satisfy the equation of curve $a{{x}^{2}}+2hxy+b{{y}^{2}}=1$. So, the values of x and y will satisfy this equation of curve, because the line is passing through the curve. So, we can write
$a{{\left( {{x}_{1}}+r\cos \theta \right)}^{2}}+2h\left( {{x}_{1}}+r\cos \theta \right)\left( {{y}_{1}}+r\sin \theta \right)+b{{\left( {{y}_{1}}+r\sin \theta \right)}^{2}}=1$
We can write the above equation as
$a{{x}_{1}}^{2}+a{{r}^{2}}{{\cos }^{2}}\theta +2ar{{x}_{1}}\cos \theta +2h{{x}_{1}}{{y}_{1}}+2h{{x}_{1}}r\sin \theta +2h{{y}_{1}}r\cos \theta +2h{{r}^{2}}\cos \theta \sin \theta +b{{y}_{1}}^{2}+b{{r}^{2}}{{\sin }^{2}}\theta +2b{{y}_{1}}r\sin \theta =1$
After rearranging the terms, we can write above equation as
$\Rightarrow {{r}^{2}}\left( a{{\cos }^{2}}\theta +2h\cos \theta \sin \theta +b{{\sin }^{2}}\theta \right)+r\left( 2a{{x}_{1}}\cos \theta +2h{{x}_{1}}\sin \theta +2h{{y}_{1}}\cos \theta +2b{{y}_{1}}\sin \theta \right)+\left( a{{x}_{1}}^{2}+2h{{x}_{1}}{{y}_{1}}+b{{y}_{1}}^{2}-1 \right)=0$ Now, we can see that the above equation is quadratic in r.
If we find the values of r, then we will get the value of PQ and PR.
That means the roots of the above equation will be PQ and PR.
As we know that the product of roots of the quadratic equation is a constant term of the quadratic equation divided by the coefficient of the quadratic term of the equation.
So, we can write
$PQ\times PR=\dfrac{\left( a{{x}_{1}}^{2}+2h{{x}_{1}}{{y}_{1}}+b{{y}_{1}}^{2}-1 \right)}{\left( a{{\cos }^{2}}\theta +2h\cos \theta \sin \theta +b{{\sin }^{2}}\theta \right)}$
If the equation $a{{x}_{1}}^{2}+2h{{x}_{1}}{{y}_{1}}+b{{y}_{1}}^{2}-1$ is zero, then we can say that the point P $\left( {{x}_{1}},{{y}_{1}} \right)$ lies on the curve. So, the equation $a{{x}_{1}}^{2}+2h{{x}_{1}}{{y}_{1}}+b{{y}_{1}}^{2}-1$ cannot be zero.
We have to make the $PQ\times PR$ independent of slope or we can say independent of$\theta$ to prove that the curve is a circle.
So, from the equation $a{{\cos }^{2}}\theta +2h\cos \theta \sin \theta +b{{\sin }^{2}}\theta$, we can write this using the formula ${{\cos }^{2}}\theta =1-{{\sin }^{2}}\theta$ as
$\Rightarrow a\left( 1-{{\sin }^{2}}\theta \right)+2h\cos \theta \sin \theta +b{{\sin }^{2}}\theta$
The above equation can also be written as
$\Rightarrow a+2h\cos \theta \sin \theta +\left( b-a \right){{\sin }^{2}}\theta$
The above equation can also be written as
$\Rightarrow a+\sin \theta \left[ 2h\cos \theta +\left( b-a \right)\sin \theta \right]$
The above term should be independent of $\theta$.
So, the value of 2h should be zero and (b-a) should be zero.
Hence, we can say that
h=0 and a=b
By putting the value of h as zero and putting the value of b as in the equation of the curve $a{{x}^{2}}+2hxy+b{{y}^{2}}=1$, we get
$a{{x}^{2}}+2(0)xy+a{{y}^{2}}=1$
The above equation can also be written as
${{x}^{2}}+{{y}^{2}}=\dfrac{1}{a}$
Hence, we can say that the above equation is a circle.
Therefore, we have proved that the equation of a curve is a circle when the term $PQ\times PR$ is independent of slope of the line PQ.

Note: We should have a better knowledge in geometry to solve this type of question.
Remember that if the point of a line is given as (a,b) and the angle of inclination of the line is $\theta$, then equation of line will be $\dfrac{y-b}{\sin \theta }=\dfrac{x-a}{\cos \theta }=r$, where r is distance from the point (a,b) to any point on the line. Don’t forget that if quadratic equation is in the form of$a{{x}^{2}}+bx+c=0$, then sum of roots of the equation will be $\dfrac{-b}{a}$ and the product of the roots of equation will be $\dfrac{c}{a}$.
Don’t forget the formula that: ${{\cos }^{2}}\theta +{{\sin }^{2}}\theta =1$, from here we can write ${{\cos }^{2}}\theta +{{\sin }^{2}}\theta =1$ which we have used in the above solution.
And always remember that the equation of the circle is ${{x}^{2}}+{{y}^{2}}={{a}^{2}}$, where a is any constant and the radius of the circle.