Question

Consider a corner atom of Ist layer of an HCP unit cell showing alternate AA layers. Find

(i) Find identical atoms (III layer) with respect to the distances from the atom 1. (ii) Arrange the distances in ascending order.

Answer 1

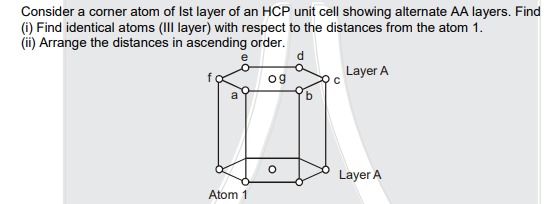
(i) Identical atoms (III layer) with respect to the distances from Atom 1:

• Atoms b, f, g are at the same distance from Atom 1 ($a\sqrt{11/3}$).
• Atoms c, e are at the same distance from Atom 1 ($a\sqrt{17/3}$).

(ii) Distances in ascending order: Let 'a' be the lattice parameter (nearest neighbor distance). For an ideal HCP, the height $c = a\sqrt{8/3}$.

1. Distance to atom 'a' (directly above Atom 1): $D_{1a} = c = a\sqrt{8/3}$.
2. Distance to atoms 'b', 'f', and 'g' (adjacent corner atoms and central atom in the top layer relative to Atom 1's vertical projection): $D_{1b} = D_{1f} = D_{1g} = \sqrt{a^2 + c^2} = \sqrt{a^2 + 8a^2/3} = a\sqrt{11/3}$.
3. Distance to atoms 'c' and 'e' (next-nearest corner atoms in the top layer relative to Atom 1's vertical projection): $D_{1c} = D_{1e} = \sqrt{3a^2 + c^2} = \sqrt{3a^2 + 8a^2/3} = a\sqrt{17/3}$.
4. Distance to atom 'd' (opposite corner atom in the top layer relative to Atom 1's vertical projection): $D_{1d} = \sqrt{4a^2 + c^2} = \sqrt{4a^2 + 8a^2/3} = a\sqrt{20/3}$.

Arranging these distances in ascending order: $a\sqrt{8/3} < a\sqrt{11/3} < a\sqrt{17/3} < a\sqrt{20/3}$

Thus, the ascending order of distances is: $D_{1a} < D_{1b} = D_{1f} = D_{1g} < D_{1c} = D_{1e} < D_{1d}$.

Answer 2

The problem requires calculating distances between atoms in an HCP unit cell. The key is to recognize the geometry of the HCP structure and use the given lattice parameters to determine the coordinates of the atoms. Then, the distance formula is applied to find the distances between the corner atom and the other atoms in the third layer. Finally, the distances are compared and arranged in ascending order. The ideal HCP ratio $c/a = \sqrt{8/3}$ is crucial for simplifying the calculations. Understanding the symmetry of the HCP lattice is also important for identifying atoms that are equidistant from the reference atom.