Question
Question: Consider a concave mirror and a convex lens (refractive index \( = 1.5\)) of focal length \(10{\text...
Consider a concave mirror and a convex lens (refractive index =1.5) of focal length 10cm each, separated by a distance of 50cm in air (refractive index =1) as shown in the figure. An object is placed at a distance of 15cm from the mirror. Its erect image formed by this combination has magnification M1. When the set-up is kept in a medium of refractive index 67, the magnification becomes M2. The magnitude M1M2 is
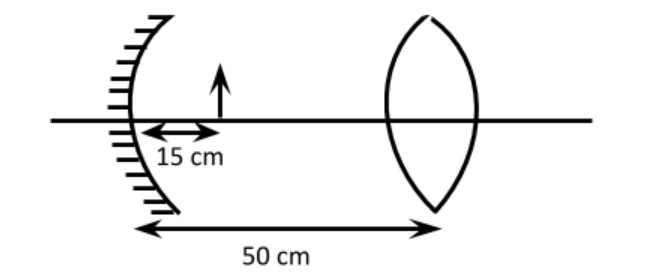
Solution
The first image from reflection by a spherical concave mirror can be found from mirror formula.
Formula used:
v1+u1=f1 v1−u1=f1 m=uv M=m1×m2
Complete step by step solution:
Given data,
For concave mirror
u=−15cm, f=−10cm
As we know,
v1+u1=f1
∴v1+−151=−101 ⇒v1=10−1+151=15010−15 ⇒v=−30cm
Dividing (1) by (2)
fairfliquid=23×76−121 =47
fliquid=47×10 =470cm
The first image will act as an object for lens and its position can be found using lens formula,
v1−u1=f1
Given:
u=−20cm, f=470cm
∴v1−−201=4701
⇒v1×704=140080−70
⇒v=140cm
Magnification is given by m′=uv=−20140=−7
Total magnification m2=−2×−7=14
Hence, m1m2=214=7
Note: Focal length of lens depends on the medium in which the whole experiment is done. Students must be careful while taking sign convention.
