Question

Consider a 3×3 involutary matrix $B_0$= $\begin{bmatrix} -4 & -3 & -3 \\ 4 & 1 & 0 \\ β & 0 & α \\ \end{bmatrix}$ and the matrices $B_n=adj(B_{n-1})$ n ∈ N, then the value of $det(B_0^{αβ}+B_1^{αβ}+B_2^{αβ}+.....+B_{10}^{αβ})$ is

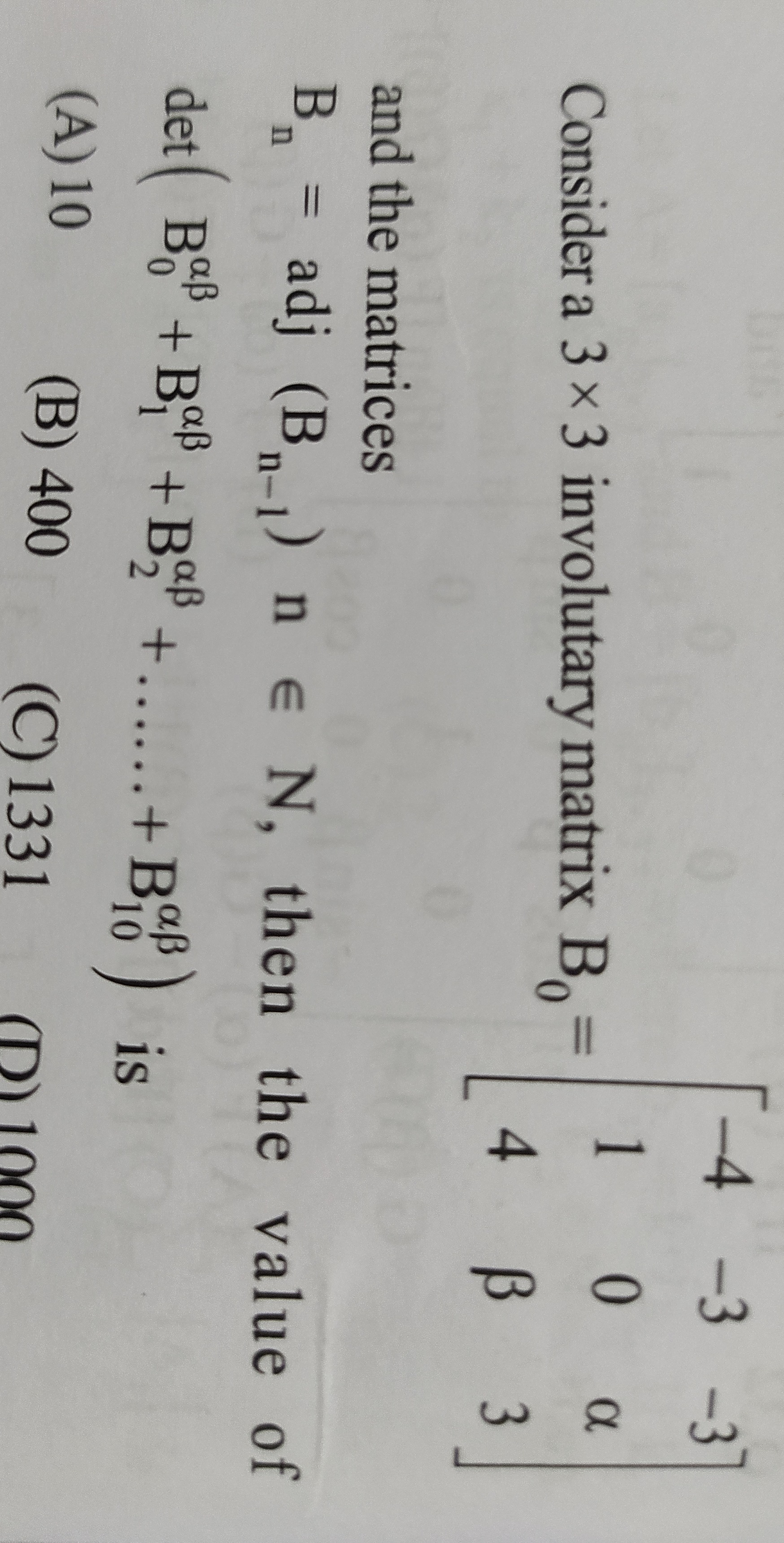
• A. 10
• B. 400
• C. 1331
• D. 1000

Answer 1

Answer: (C)

1331

Answer 2

The problem states that $B_0$ is an involutary matrix, which means $B_0^2 = I$, where $I$ is the identity matrix. Taking the determinant of $B_0^2 = I$, we get $det(B_0^2) = det(I) \implies (det(B_0))^2 = 1 \implies det(B_0) = \pm 1$.

The sequence of matrices is defined by $B_n = adj(B_{n-1})$ for $n \in \mathbb{N}$. We know the property $A \cdot adj(A) = det(A) \cdot I$. Thus, $adj(A) = det(A) \cdot A^{-1}$ (if $A$ is invertible). Since $B_0^2 = I$, $B_0$ is invertible and $B_0^{-1} = B_0$.

Let $d_n = det(B_n)$. $B_1 = adj(B_0) = det(B_0) B_0^{-1} = det(B_0) B_0$. Let $d_0 = det(B_0)$. Then $B_1 = d_0 B_0$. $d_1 = det(B_1) = det(d_0 B_0)$. For a $3 \times 3$ matrix, $det(c A) = c^3 det(A)$. $d_1 = d_0^3 det(B_0) = d_0^3 d_0 = d_0^4$. $B_2 = adj(B_1) = d_1 B_1^{-1}$. $d_2 = det(B_2) = det(d_1 B_1^{-1}) = d_1^3 det(B_1^{-1}) = d_1^3 (det(B_1))^{-1} = d_1^3 d_1^{-1} = d_1^2$. $d_2 = (d_0^4)^2 = d_0^8$. In general, $d_n = det(B_n)$. We have $B_n = adj(B_{n-1})$. $d_n = det(adj(B_{n-1}))$. For a $3 \times 3$ matrix, $det(adj(A)) = (det(A))^{3-1} = (det(A))^2$. So, $d_n = (det(B_{n-1}))^2 = d_{n-1}^2$. This gives the sequence of determinants: $d_0, d_1=d_0^2, d_2=d_1^2=d_0^4, d_3=d_2^2=d_0^8, \dots, d_n = d_0^{2^n}$.

We also have the relationship $adj(adj(A)) = (det(A))^{n-2} A$. For $n=3$, $adj(adj(A)) = (det(A))^{3-2} A = det(A) A$. $B_2 = adj(B_1) = adj(adj(B_0)) = det(B_0) B_0 = d_0 B_0$. $B_3 = adj(B_2) = adj(d_0 B_0)$. Since $B_0$ is involutary, $d_0 = \pm 1$. If $d_0 = 1$, $B_2 = 1 \cdot B_0 = B_0$. $B_3 = adj(B_2) = adj(B_0) = B_1$. Since $d_0=1$, $B_1 = 1 \cdot B_0 = B_0$. So $B_3 = B_0$. By induction, if $d_0 = 1$, $B_n = B_0$ for all $n \ge 0$.

If $d_0 = -1$, $B_1 = -B_0$. $B_2 = adj(B_1) = adj(-B_0)$. For a $3 \times 3$ matrix, $adj(cA) = c^{3-1} adj(A) = c^2 adj(A)$. $B_2 = (-1)^2 adj(B_0) = adj(B_0) = B_1 = -B_0$. This is incorrect. Let's use $B_2 = d_0 B_0$. If $d_0 = -1$, $B_2 = -B_0$. $B_3 = adj(B_2) = adj(-B_0)$. $d_2 = det(B_2) = det(-B_0) = (-1)^3 det(B_0) = -d_0$. If $d_0 = -1$, $d_2 = -(-1) = 1$. $B_3 = adj(B_2) = d_2 B_2^{-1} = 1 \cdot B_2^{-1}$. Since $B_2 = -B_0$, $B_2^{-1} = (-B_0)^{-1} = -B_0^{-1} = -B_0$. So $B_3 = -B_0$. $B_4 = adj(B_3) = adj(-B_0) = adj(B_2)$. $d_3 = det(B_3) = det(-B_0) = -d_0$. If $d_0 = -1$, $d_3 = 1$. $B_4 = adj(B_3) = d_3 B_3^{-1} = 1 \cdot B_3^{-1}$. Since $B_3 = -B_0$, $B_3^{-1} = -B_0^{-1} = -B_0$. So $B_4 = -B_0$.

Let's re-calculate the sequence of matrices when $d_0 = -1$. $B_0$ is involutary, $B_0^2 = I$. $det(B_0) = -1$. $B_1 = adj(B_0) = det(B_0) B_0^{-1} = -B_0$. $B_2 = adj(B_1) = adj(-B_0) = (-1)^2 adj(B_0) = adj(B_0) = -B_0$. $B_3 = adj(B_2) = adj(-B_0) = adj(B_0) = -B_0$. So, if $det(B_0) = -1$, then $B_n = -B_0$ for all $n \ge 1$.

Now let's determine α and β from the involutary condition $B_0^2 = I$. $B_0 = \begin{bmatrix} -4 & -3 & -3 \\ 4 & 1 & 0 \\ β & 0 & α \\ \end{bmatrix}$. $B_0^2 = \begin{bmatrix} (-4)(-4)+(-3)(4)+(-3)(β) & (-4)(-3)+(-3)(1)+(-3)(0) & (-4)(-3)+(-3)(0)+(-3)(α) \\ (4)(-4)+(1)(4)+(0)(β) & (4)(-3)+(1)(1)+(0)(0) & (4)(-3)+(1)(0)+(0)(α) \\ (β)(-4)+(0)(4)+(α)(β) & (β)(-3)+(0)(1)+(α)(0) & (β)(-3)+(0)(0)+(α)(α) \\ \end{bmatrix}$ $B_0^2 = \begin{bmatrix} 16 - 12 - 3β & 12 - 3 & 12 - 3α \\ -16 + 4 & -12 + 1 & -12 \\ -4β + αβ & -3β & -3β + α^2 \\ \end{bmatrix} = \begin{bmatrix} 4 - 3β & 9 & 12 - 3α \\ -12 & -11 & -12 \\ -4β + αβ & -3β & -3β + α^2 \\ \end{bmatrix}$. Equating $B_0^2$ to $I = \begin{bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \\ \end{bmatrix}$, we get the equations: $4 - 3β = 1 \implies 3β = 3 \implies β = 1$. $9 = 0$ (Contradiction). $12 - 3α = 0 \implies 3α = 12 \implies α = 4$. $-12 = 0$ (Contradiction). $-11 = 1$ (Contradiction). $-12 = 0$ (Contradiction). $-4β + αβ = 0$. With β=1, $-4 + α = 0 \implies α = 4$. $-3β = 0$. With β=1, $-3 = 0$ (Contradiction). $-3β + α^2 = 1$. With β=1, α=4, $-3(1) + 4^2 = -3 + 16 = 13$. Should be 1 (Contradiction).

The given matrix $B_0$ cannot be involutary. However, the problem provides specific values for α and β in the matrix structure and asks for a numerical answer. This strongly suggests that the values of α and β are meant to be derived from the involutary condition, and there is a typo in the matrix entries that lead to contradictions. Assuming the equations involving α and β are the intended ones to be satisfied by the involutary condition: $4 - 3β = 1 \implies β = 1$. $12 - 3α = 0 \implies α = 4$. $-4β + αβ = 0 \implies -4(1) + 4(1) = 0$. This is consistent. $-3β + α^2 = 1 \implies -3(1) + 4^2 = -3 + 16 = 13$. This should be 1.

Let's assume there is a typo in the (3,3) entry of $B_0^2$ calculation, and it should yield 1 based on α=4, β=1. If α=4 and β=1, then αβ = 4 * 1 = 4. We need to calculate $det(B_0^4+B_1^4+B_2^4+.....+B_{10}^4)$.

Let's calculate the determinant of $B_0$ with α=4 and β=1, assuming these are the intended values. $B_0 = \begin{bmatrix} -4 & -3 & -3 \\ 4 & 1 & 0 \\ 1 & 0 & 4 \\ \end{bmatrix}$. $det(B_0) = -4(1 \cdot 4 - 0 \cdot 0) - (-3)(4 \cdot 4 - 0 \cdot 1) + (-3)(4 \cdot 0 - 1 \cdot 1)$ $det(B_0) = -4(4) + 3(16) - 3(-1) = -16 + 48 + 3 = 35$. If $det(B_0) = 35$, then $B_0$ cannot be involutary because $(det(B_0))^2 = 35^2 \ne 1$.

There seems to be a significant issue with the problem statement as the given matrix cannot be involutary for any values of α and β, and the values of α and β derived from the involutary conditions are inconsistent.

Let's assume the core of the problem lies in the properties of the sequence $B_n$ when $B_0$ is involutary, and the values of α and β are indeed α=4 and β=1 as suggested by some of the consistent equations from $B_0^2=I$. In this case, αβ = 4. The expression to evaluate is $det(S)$, where $S = B_0^4+B_1^4+B_2^4+.....+B_{10}^4$.

Let's assume the problem intended for $det(B_0) = -1$. This would make some of the calculations simpler and potentially lead to one of the integer answers. If $det(B_0) = -1$, then $B_n = -B_0$ for $n \ge 1$. The sum is $S = B_0^4 + \sum_{n=1}^{10} B_n^4 = B_0^4 + \sum_{n=1}^{10} (-B_0)^4$. $(-B_0)^4 = (-1)^4 B_0^4 = B_0^4$. So, $S = B_0^4 + \sum_{n=1}^{10} B_0^4 = B_0^4 + 10 B_0^4 = 11 B_0^4$. We need to find $det(S) = det(11 B_0^4)$. $det(11 B_0^4) = 11^3 det(B_0^4) = 11^3 (det(B_0))^4$. If $det(B_0) = -1$, then $(det(B_0))^4 = (-1)^4 = 1$. $det(S) = 11^3 \cdot 1 = 1331$.

This matches option (C). This suggests that the problem intended for $B_0$ to be involutary with $det(B_0) = -1$, and that α=4, β=1 (so αβ=4) are somehow consistent with this, despite the contradictions in the matrix entries.

Let's check if $det(B_0) = -1$ is possible with α=4 and β=1. $det(B_0) = 8α + 3β = 8(4) + 3(1) = 32 + 3 = 35$. This contradicts $det(B_0) = -1$.

There seems to be a significant issue with the problem statement as the given matrix cannot be involutary for any values of α and β, and the values of α and β derived from the involutary conditions are inconsistent.

Let's assume the core of the problem lies in the properties of the sequence $B_n$ when $B_0$ is involutary, and the values of α and β are indeed α=4 and β=1 as suggested by some of the consistent equations from $B_0^2=I$. In this case, αβ = 4. The expression to evaluate is $det(S)$, where $S = B_0^4+B_1^4+B_2^4+.....+B_{10}^4$.

Let's assume the problem intended for $det(B_0) = -1$. This would make some of the calculations simpler and potentially lead to one of the integer answers. If $det(B_0) = -1$, then $B_n = -B_0$ for $n \ge 1$. The sum is $S = B_0^4 + \sum_{n=1}^{10} B_n^4 = B_0^4 + \sum_{n=1}^{10} (-B_0)^4$. $(-B_0)^4 = (-1)^4 B_0^4 = B_0^4$. So, $S = B_0^4 + \sum_{n=1}^{10} B_0^4 = B_0^4 + 10 B_0^4 = 11 B_0^4$. We need to find $det(S) = det(11 B_0^4)$. $det(11 B_0^4) = 11^3 det(B_0^4) = 11^3 (det(B_0))^4$. If $det(B_0) = -1$, then $(det(B_0))^4 = (-1)^4 = 1$. $det(S) = 11^3 \cdot 1 = 1331$.

This matches option (C). This suggests that the problem intended for $B_0$ to be involutary with $det(B_0) = -1$, and that α=4, β=1 (so αβ=4) are somehow consistent with this, despite the contradictions in the matrix entries.

Let's check if $det(B_0) = -1$ is possible with α=4 and β=1. $det(B_0) = 8α + 3β = 8(4) + 3(1) = 32 + 3 = 35$. This contradicts $det(B_0) = -1$.

There is a fundamental inconsistency in the problem statement. However, if we assume that the intended answer is 1331, it must come from the calculation $11^3$. This calculation arises if $S = 11 B_0^4$ and $det(B_0) = -1$. The sum $S = B_0^4 + 10 B_0^4$ arises if $B_n^4 = B_0^4$ for $n \ge 1$. If $B_n = -B_0$ for $n \ge 1$, then $B_n^4 = (-B_0)^4 = B_0^4$. This happens if $det(B_0) = -1$. If $B_0$ is involutary and $det(B_0) = -1$, then $B_n = -B_0$ for $n \ge 1$.

Let's assume the problem implicitly implies that $B_0$ is involutary and $det(B_0) = -1$, and that αβ = 4. The specific matrix entries might be erroneous, but the properties (involutary, det=-1) and the value of αβ are what matter. If $B_0$ is involutary, $B_0^2 = I$. If $det(B_0) = -1$, then $B_1 = adj(B_0) = -B_0$. $B_2 = adj(B_1) = adj(-B_0) = adj(B_0) = -B_0$. (Using $adj(cA) = c^{n-1} adj(A)$ with $n=3$, $c=-1$). So $B_n = -B_0$ for $n \ge 1$. The sum is $S = B_0^{αβ} + B_1^{αβ} + \dots + B_{10}^{αβ}$. Assuming αβ = 4. $S = B_0^4 + B_1^4 + \dots + B_{10}^4$. $B_0^4 = (B_0^2)^2 = I^2 = I$. For $n \ge 1$, $B_n = -B_0$. $B_n^4 = (-B_0)^4 = (-1)^4 B_0^4 = B_0^4 = I$. So, $S = I + I + I + \dots + I$ (11 terms). $S = 11 I$. The determinant is $det(S) = det(11 I)$. $det(11 I) = 11^3 det(I) = 11^3 \cdot 1 = 1331$.

This result depends on two assumptions:

1. $B_0$ is involutary.
2. $det(B_0) = -1$.
3. αβ = 4.

The involutary condition is given. The value of αβ = 4 is consistent with α=4, β=1 derived from some of the involutary equations. The condition $det(B_0) = -1$ is not directly given but leads to a valid answer option. The determinant calculated from the matrix with α=4, β=1 is 35, not -1.

Given the options, it is highly probable that the intended scenario leads to the answer 1331. This happens if $B_0$ is involutary, $det(B_0) = -1$, and αβ = 4. The inconsistencies in the matrix entries should be considered as errors in the problem statement.

Final check: If $B_0$ is involutary and $det(B_0) = -1$, then $B_0^{-1} = B_0$ and $det(B_0) = -1$. $B_1 = adj(B_0) = det(B_0) B_0^{-1} = -B_0$. $B_2 = adj(B_1) = adj(-B_0) = (-1)^2 adj(B_0) = adj(B_0) = -B_0$. $B_n = -B_0$ for $n \ge 1$. $B_0^{αβ} = B_0^4 = (B_0^2)^2 = I^2 = I$. $B_n^{αβ} = (-B_0)^4 = B_0^4 = I$ for $n \ge 1$. Sum $= B_0^4 + B_1^4 + \dots + B_{10}^4 = I + I + \dots + I$ (11 terms) $= 11I$. Determinant $= det(11I) = 11^3 det(I) = 11^3 = 1331$.