Question

Consider a 10-cm long piece of a wire which carries a current of 10A. Find the magnitude of the magnetic field due to the piece at a point which makes an equilateral triangle with the ends of the piece.

Answer 1

in this question we will use the relation between magnetic field, current in the wire, length of wire, angle and the radius. Now, substituting the given values in the expression will give us the required result. Further, we will discuss the basics of magnetic field and the rules to find the direction of magnetic field.
Formula used:
$B = \dfrac{{{\mu _0}I}}{{4\pi r}}\left( {\sin {\phi _1} + \sin {\phi _2}} \right)$

Complete answer:
Here, we will use the expression, which gives us magnetic fields. This is also called Biot- Savart’s law.

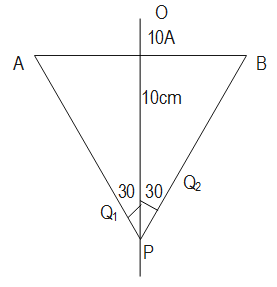
As we know, magnetic field B is given by:
$B = \dfrac{{{\mu _0}I}}{{4\pi r}}\left( {\sin {\phi _1} + \sin {\phi _2}} \right)$
Now, by substituting the given values in above equation, we get:
\eqalign{ & B = \dfrac{{{{10}^{ - 7}} \times 10 \times 1}}{{\dfrac{{\sqrt 3 }}{2} \times 0.1}} \cr & \Rightarrow B = \dfrac{{2 \times {{10}^{ - 5}}}}{{1.732}} \cr}
$\therefore B = 1.154 \times {10^{ - 5}}T = 11.54\mu T$
Therefore, we get the required result which gives us the magnitude of the magnetic field due to the piece at a point which makes an equilateral triangle with the ends of the piece.

Additional information:
As we know that magnetic field is defined as a vector field that tells us the magnetic influence on moving electric charges, electric currents, and magnetized materials also. Also, we should know that a charge that is moving in a magnetic field experiences a force that is perpendicular to its town velocity and to the magnetic field.
There are two rules given, to find the direction of magnetic field:
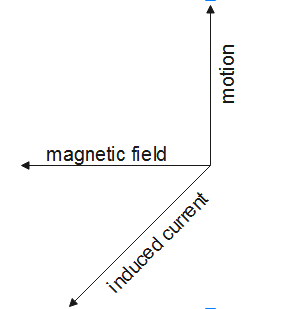
Fleming’s right-hand rule can be understood as: from this rule, if we Stretch the thumb, forefinger and middle finger of our right hand such that they are mutually perpendicular to each other. Here, if the forefinger point indicates the direction of the magnetic field and the thumb indicates the direction of motion of the conductor, then the middle finger will indicate the direction of induced current in the conductor.

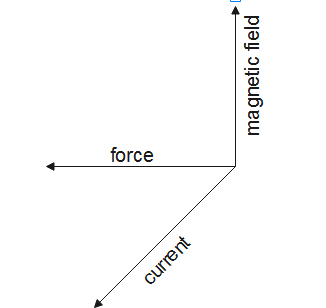
Fleming’s left-hand rule: from this rule if we Stretch our thumb, forefinger and middle finger of the left hand such that all these fingers are mutually perpendicular to each other. So, if the forefinger points in the direction of the magnetic field and the middle finger indicates the direction of the current, then the thumb will indicate the direction of motion or the force on the conductor.

Note:
We should know that Fleming's left-hand rule gives the direction of magnetic force acting on a conductor whereas; Fleming’s right-hand rule gives us the direction of induced current. Further, the magnetic field is measured in Tesla T. It is also given by Weber per meter square.