Question
Question: Conductivity of a saturated solution of $Mg_3(PO_4)_2$ is $1.2 \times 10^{-5} S cm^{-1}$. Limiting e...
Conductivity of a saturated solution of Mg3(PO4)2 is 1.2×10−5Scm−1. Limiting equivalent conductivities of MgCl2,Na3PO4 and NaCl are 160, 140 and 100 eqScm2 respectively. Find Ksp of Mg3(PO4)2
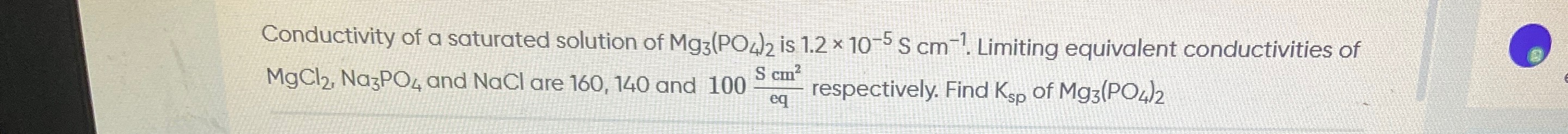
1.08×10−23
Solution
To find the Ksp of Mg3(PO4)2, we need to follow these steps:
- Calculate the limiting equivalent conductivity (Λeq∘) of Mg3(PO4)2.
- Use the conductivity of the saturated solution and Λeq∘ to find the molar solubility (S) of Mg3(PO4)2.
- Calculate Ksp from the molar solubility (S).
Step 1: Calculate Λeq∘ for Mg3(PO4)2
According to Kohlrausch's Law of independent migration of ions, the limiting equivalent conductivity of an electrolyte is the sum of the limiting equivalent conductivities of its constituent ions. We are given:
Λeq∘(MgCl2)=λeq∘(Mg2+)+λeq∘(Cl−)=160eqScm2
Λeq∘(Na3PO4)=λeq∘(Na+)+λeq∘(PO43−)=140eqScm2
Λeq∘(NaCl)=λeq∘(Na+)+λeq∘(Cl−)=100eqScm2
We need Λeq∘(Mg3(PO4)2)=λeq∘(Mg2+)+λeq∘(PO43−). This can be obtained by:
Λeq∘(Mg3(PO4)2)=Λeq∘(MgCl2)+Λeq∘(Na3PO4)−Λeq∘(NaCl)
Λeq∘(Mg3(PO4)2)=160+140−100=200eqScm2
Step 2: Calculate the molar solubility (S) of Mg3(PO4)2
The relationship between conductivity (κ), equivalent conductivity (Λeq), and equivalent concentration (Ceq) is:
κ=1000Λeq×Ceq
where κ is in Scm−1, Λeq is in Scm2eq−1, and Ceq is in eq/L. For a sparingly soluble salt like Mg3(PO4)2 in a saturated solution, we can approximate Λeq≈Λeq∘.
Given κ=1.2×10−5Scm−1.
Ceq=Λeq∘κ×1000
Ceq=200Scm2eq−11.2×10−5Scm−1×1000
Ceq=2001.2×10−2=6×10−5eq/L
Now, relate the equivalent concentration (Ceq) to the molar solubility (S). For Mg3(PO4)2, the total positive charge is 3×(+2)=+6, and the total negative charge is 2×(−3)=−6. Therefore, 1 mole of Mg3(PO4)2 corresponds to 6 equivalents. So, Ceq=6S
6×10−5eq/L=6S
S=1.0×10−5mol/L
Step 3: Calculate Ksp of Mg3(PO4)2
The dissolution equilibrium for Mg3(PO4)2 is:
Mg3(PO4)2(s)⇌3Mg2+(aq)+2PO43−(aq)
If the molar solubility is S, then at equilibrium:
[Mg2+]=3S
[PO43−]=2S
The solubility product constant (Ksp) is given by:
Ksp=[Mg2+]3[PO43−]2
Ksp=(3S)3(2S)2
Ksp=(27S3)(4S2)
Ksp=108S5
Substitute the value of S:
Ksp=108×(1.0×10−5)5
Ksp=108×(1.05×(10−5)5)
Ksp=108×1.0×10−25
Ksp=1.08×10−23
The final answer is 1.08×10−23.
Explanation of the solution:
- Kohlrausch's Law: Λeq∘(Mg3(PO4)2)=Λeq∘(MgCl2)+Λeq∘(Na3PO4)−Λeq∘(NaCl)=160+140−100=200eqScm2.
- Solubility from Conductivity: Use κ=1000Λeq∘×Ceq. Given κ=1.2×10−5Scm−1, Ceq=2001.2×10−5×1000=6×10−5eq/L. Since 1 mol of Mg3(PO4)2=6 eq, molar solubility S=6Ceq=66×10−5=1.0×10−5mol/L.
- Ksp Calculation: For Mg3(PO4)2⇌3Mg2++2PO43−, Ksp=[Mg2+]3[PO43−]2=(3S)3(2S)2=108S5. Substitute S=1.0×10−5mol/L: Ksp=108×(1.0×10−5)5=108×10−25=1.08×10−23.
