Question

Compute the larger area bounded by $y=4+3x-{{x}^{2}}$and the coordinate axes.

Answer 1

Hint: Try to find where the curve cuts the $x$ axis. First try to make a rough sketch. Then find the area under the curve using integral.

Note that a quadratic function always represents a parabola.
So, first of all let’s try plotting the curve considering various values,
Note that at $x=0,y=4$
And at $y=0,\left( x-4 \right)\left( x+1 \right)=0$ or $x=4,-1$
Use the above observations to plot the graph.

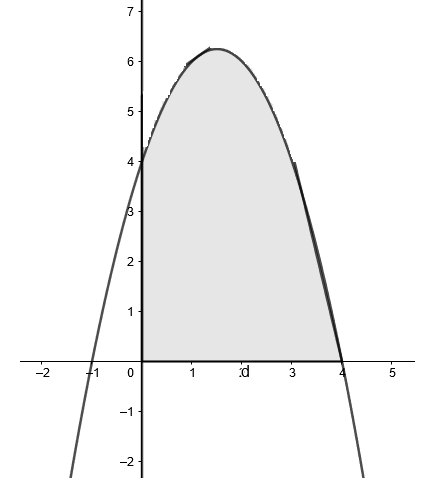
The shaded region is the required area.
Hence, we can now find the area by integrating the function from $x=0$ to $x=4$.
The formula of finding the area enclosed by $f(x)$ between $x=a$ and $x=b$ can be written as $=|\int\limits_{a}^{b}{f(x)dx|}$.
So the required area under the curve is,
$\text{Area}=\int\limits_{0}^{4}{\left( 4+3x-{{x}^{2}} \right)dx}$
Now we know the integration of sum of functions is sum of individual integration of the functions, i.e.,
$\text{Area}=\int\limits_{0}^{4}{4dx}+\int\limits_{0}^{4}{\left( 3x \right)dx}-\int\limits_{0}^{4}{\left( {{x}^{2}} \right)dx}$
On integrating, we get
$Area=\left[ 4x \right]_{0}^{4}+3\left[ \dfrac{{{x}^{2}}}{2} \right]_{0}^{4}-\left[ \dfrac{{{x}^{3}}}{3} \right]_{0}^{4}$
Applying the limits, we get
$Area=\left[ 4(4)-4(0) \right]+3\left[ \dfrac{{{4}^{2}}}{2}-\dfrac{{{0}^{2}}}{2} \right]-\left[ \dfrac{{{4}^{3}}}{3}-\dfrac{{{0}^{2}}}{3} \right]$
On solving, we get
$Area=16+24-\dfrac{64}{3}$
Taking the LCM, we get
$Area=\dfrac{40\times 3-64}{3}$
$Area=\dfrac{40\times 3-64}{3}=\dfrac{120-64}{3}$
$Area=\dfrac{56}{3}$sq. units
Therefore the area under the curve is $\dfrac{56}{3}$ sq. units.
Note: The possibility of mistake is that students might take the lower limit as $-1$ considering the curve and forget to note that it is asked to find the area of the curve with the coordinate axes, so the lower limit will be $0$.