Question
Question: Two laser beams of wavelength $\lambda$ are incident at angle of $\theta_1$ and $\theta_2$ on a scre...
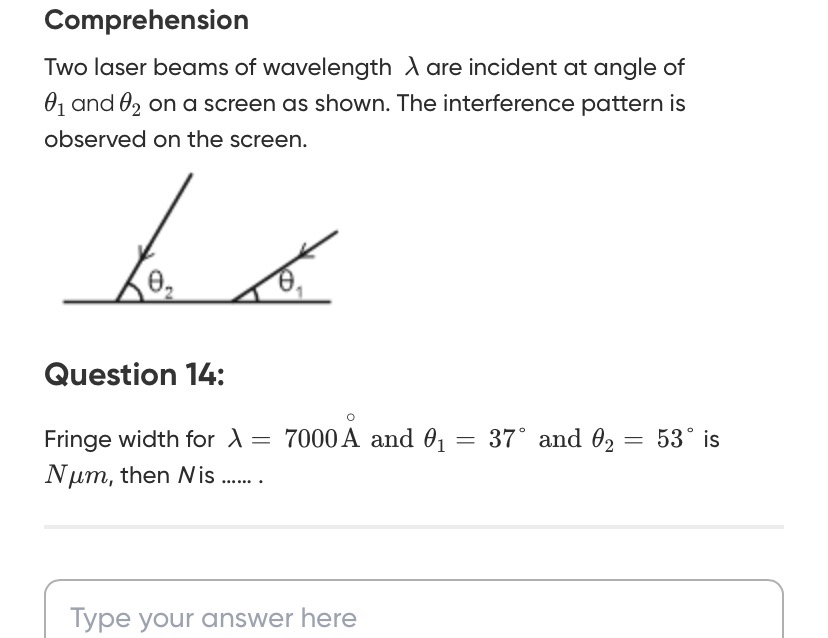
Two laser beams of wavelength λ are incident at angle of θ1 and θ2 on a screen as shown. The interference pattern is observed on the screen. Fringe width for λ=7000A˚ and θ1=37∘ and θ2=53∘ is Nμm, then N is .......
1
Solution
The fringe width β in an interference pattern is generally given by the formula β=dsinαλ, where λ is the wavelength of light, d is the effective separation of the sources, and α is the angle between the two interfering beams.
In this problem, the angles θ1 and θ2 are given with respect to the screen. From the diagram, it can be inferred that the angle between the two beams is the sum of these angles, α=θ1+θ2.
Given: Wavelength, λ=7000A˚=7000×10−10m=7×10−7m. Angle θ1=37∘. Angle θ2=53∘.
The angle between the two beams is α=θ1+θ2=37∘+53∘=90∘. Therefore, sinα=sin90∘=1.
The formula for fringe width becomes β=dsin90∘λ=dλ.
We are given that the fringe width is Nμm. So, β=N×10−6m.
Substituting the value of λ: N×10−6m=d7×10−7m. N=d×10−67×10−7=d0.7.
Since the value of d (effective separation of sources) is not provided, we infer that for the problem to have a specific numerical answer, there might be an implicit assumption or a common scenario being tested. A common assumption in such problems, especially when the answer is expected to be a simple integer, is that the effective separation of the sources is equal to the wavelength of the light, i.e., d=λ.
Assuming d=λ=7000A˚=0.7μm: N=0.7μm0.7μm=1.
Thus, the fringe width is 1μm, and N=1.
