Solveeit Logo
Login

Question

Question: What is the scalar projection of $\vec{a}$ on $\vec{b}$?...

What is the scalar projection of a⃗\vec{a} on b⃗\vec{b}?

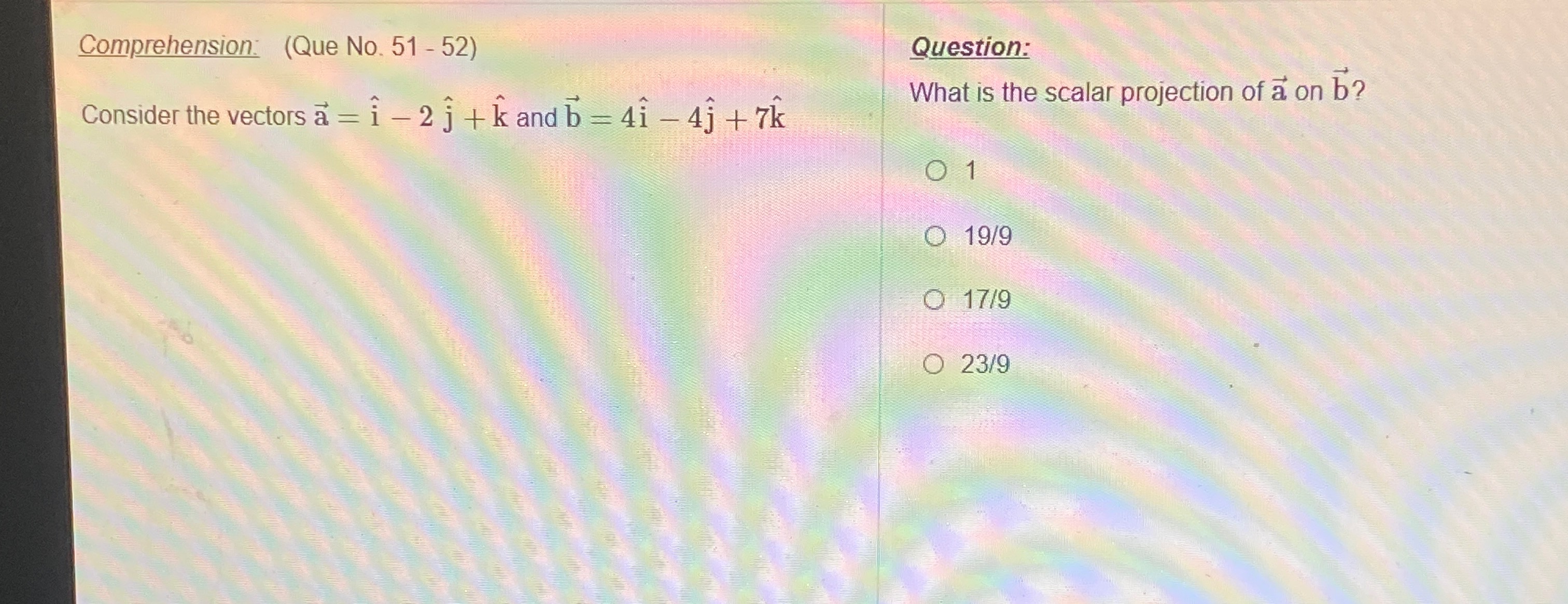
A

1

B

19/9

C

17/9

D

23/9

Answer

19/9

Explanation

Solution

The scalar projection of vector a⃗\vec{a} on vector b⃗\vec{b} is given by the formula: Scalar Projection=a⃗⋅b⃗∣b⃗∣\text{Scalar Projection} = \frac{\vec{a} \cdot \vec{b}}{|\vec{b}|}

Given vectors are: a⃗=i^−2j^+k^\vec{a} = \hat{i} - 2\hat{j} + \hat{k} b⃗=4i^−4j^+7k^\vec{b} = 4\hat{i} - 4\hat{j} + 7\hat{k}

  1. Calculate the dot product a⃗⋅b⃗\vec{a} \cdot \vec{b}: a⃗⋅b⃗=(1)(4)+(−2)(−4)+(1)(7)=4+8+7=19\vec{a} \cdot \vec{b} = (1)(4) + (-2)(-4) + (1)(7) = 4 + 8 + 7 = 19
  2. Calculate the magnitude of vector b⃗\vec{b}, i.e., ∣b⃗∣|\vec{b}|: ∣b⃗∣=(4)2+(−4)2+(7)2=16+16+49=81=9|\vec{b}| = \sqrt{(4)^2 + (-4)^2 + (7)^2} = \sqrt{16 + 16 + 49} = \sqrt{81} = 9
  3. Calculate the scalar projection of a⃗\vec{a} on b⃗\vec{b}: Scalar Projection=a⃗⋅b⃗∣b⃗∣=199\text{Scalar Projection} = \frac{\vec{a} \cdot \vec{b}}{|\vec{b}|} = \frac{19}{9}