Question

The value of the sum $|P_1 P_2|^2 + |P_1 P_3|^2 + \dots + |P_1 P_{10}|^2$ is

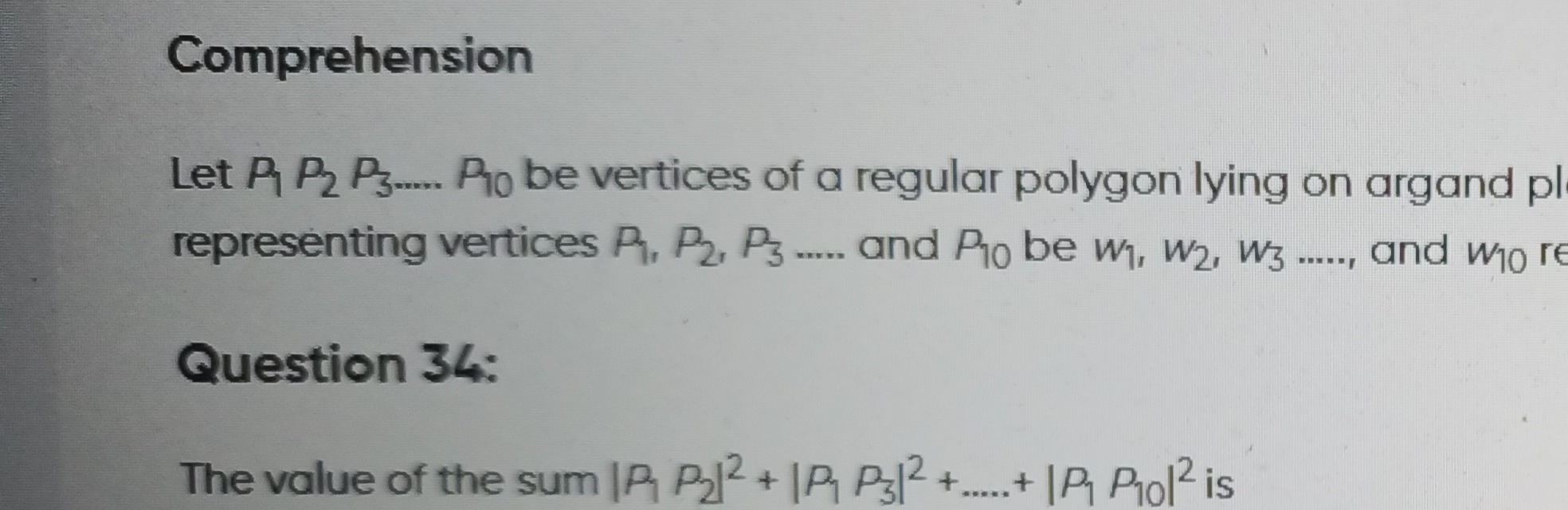
Answer 1

20

Answer 2

Let the vertices of the regular decagon be represented by complex numbers $w_1, w_2, \dots, w_{10}$. We are asked to find the sum $S = \sum_{k=2}^{10} |w_1 - w_k|^2$. For a regular $n$-gon centered at the origin with circumradius $R$, the sum of the squared distances from one vertex to all other $n-1$ vertices is $n(n-1)R^2$. In this case, $n=10$. So the sum is $10(10-1)R^2 = 10 \times 9 \times R^2 = 90R^2$.

However, a more direct theorem states that for a regular $n$-gon inscribed in a circle of radius $R$, the sum of the squared distances from any vertex to the other $n-1$ vertices is $2nR^2$. For $n=10$, the sum is $2 \times 10 \times R^2 = 20R^2$.

If we assume the vertices are the 10th roots of unity, then $R=1$. In this case, the sum is $20 \times 1^2 = 20$.