Question

Complex ${{[Fe{{L}_{6}}]}^{2+}}$ is yellow in color then expected magnetic moment (in BM) of complex will be (L $\to$ Monodentate neutral ligand) (Wavelength corresponding to pairing energy is 500 nm):
(a)- 0
(b)- $\sqrt{8}$
(c)- $\sqrt{15}$
(d)- $\sqrt{24}$

Answer 1

To find the magnetic moment we have to first, find the central metal atom in the complex and then write its electronic configuration in the ground state. Find the oxidation state of the central metal atom and write the configuration accordingly, and find the number of unpaired electrons. Use the formula $\sqrt{n(n+2)}$ to find the magnetic moment where n is the number of unpaired electrons.

Complete answer:
The given complex is:
${{[Fe{{L}_{6}}]}^{2+}}$
The central metal atom in this is iron, and the atomic number of iron is 26.
So, the electronic configuration of iron in the ground state will be:
$1{{s}^{2}}2{{s}^{2}}2{{p}^{6}}3{{s}^{2}}3{{p}^{6}}4{{s}^{2}}3{{d}^{6}}$
Given that the L (ligand) is a monodentate neutral ligand, there will be no charge on it. As the overall charge on the complex is +2, so the sum of all the oxidation states of the elements in the complex will be equal to +2. The oxidation state of iron will be:
$x+6(0)=+2$
$x=+2$
So, the oxidation state of iron is +2. The electronic configuration of iron in +2 oxidation state will be:
$1{{s}^{2}}2{{s}^{2}}2{{p}^{6}}3{{s}^{2}}3{{p}^{6}}3{{d}^{6}}$
So, the $3{{d}^{6}}$ will be represented as:

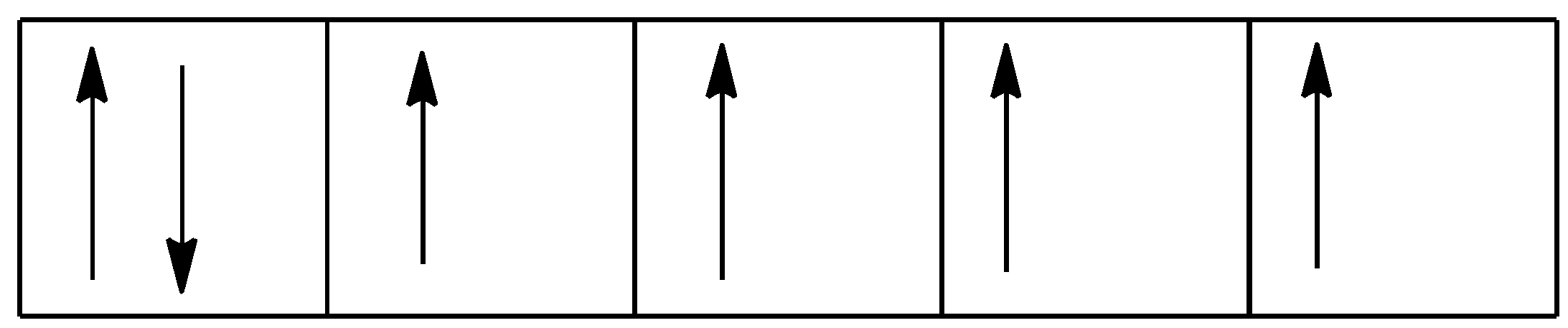
We can use the formula $\sqrt{n(n+2)}$ to find the magnetic moment where n is the number of unpaired electrons.
So, the numbers of unpaired electrons are 4. Putting this value in the formula, we get:
$\sqrt{n(n+2)}=\sqrt{4(4+2)}$
$Magnetic\text{ }moment=\sqrt{24}$

So, the correct answer is an option (d).

Note:
There will be no pairing in the complex because the energy at which the absorption occurs is 410 nm, and the minimum amount of wavelength required for the pairing is 500 nm.