Question

Complete the Venn diagram
\begin{array}{l}E = \left\\{ {21,22,23,24,25,26,27,28,29,30} \right\\}\\\A = \left\\{ {x:x\,{\rm{is}}\,{\rm{a}}\,{\rm{multiple}}\,{\rm{of}}\,3} \right\\}\\\B = \left\\{ {x:x\,{\rm{is}}\,{\rm{prime}}} \right\\}\\\C = \left\\{ {x:x\,{\rm{ < 25}}} \right\\}\end{array}

Answer 1

Here we will first find the elements of the sets given with the conditions. Then we will find the common terms between the every two groups. We will then find the common terms from all the three groups. Then we will complete the Venn diagram using the obtained elements or terms.

Complete step by step solution:
The given set of data is E = \left\\{ {21,22,23,24,25,26,27,28,29,30} \right\\}
Firstly we will find the elements of each group.
Condition of the group A is A = \left\\{ {x:x\,{\rm{is}}\,{\rm{a}}\,{\rm{multiple}}\,{\rm{of}}\,3} \right\\}. Therefore the elements in the group A is
A = \left\\{ {21,24,27,30} \right\\}
Condition of the group B is B = \left\\{ {x:x\,{\rm{is}}\,{\rm{prime}}} \right\\}. Therefore the elements in the group B is
B = \left\\{ {23,29} \right\\}
Condition of the group C is C = \left\\{ {x:x\,{\rm{ < 25}}} \right\\}. Therefore the elements in the group C is
C = \left\\{ {21,22,23,24} \right\\}
Now we will find the common term between the group A and B, we get
$A \cup B = 0$
Now we will find the common term between the group B and C, we get
B \cup C = \left\\{ {23} \right\\}
Now we will find the common term between the group A and C, we get
A \cup C = \left\\{ {21,24} \right\\}
Now we will find the common terms in all the three groups A, Band C. Therefore, we get
$A \cup B \cup C = 0$
Now we will fill these values in the Venn diagram. Therefore we get

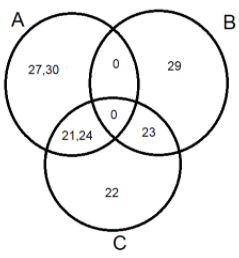
Hence, the Venn diagram is completed.

Note:
Here we should know that Venn diagram is the diagram which shows all the possible relations between different sets of data. Venn diagrams are also known as the primary diagram or logic diagram or set diagram. It is important to note that the intersection area by all the three circles is the area for the elements common in all the three groups. The areas intersected by two circles are the area for the elements which are common in those two groups. We should also remember that in the common region the data may not repeat.