Question

Complete the following statement
1. $A\cap B=B\Rightarrow B.......A$

Answer 1

We will try to find the relation between the two sets A and B. $A\cap B=B$ tells us about the total inclusion of set B inside the set A. From this, we will find the subset relation between set A and set B.

Complete step-by-step solution:
Before we solve the question, let us see what does symbol, $\cap$ means.
Let us assume we have two non - empty sets, say A and B.
Now, let A be set of first 10 natural numbers, then
$A = { 1, 2, 3, 4, 5, 6, 7, 8, ,9, 10}$
And B be set off first 5 multiples of 2, then
$B = { 2, 4, 6, 8, 10 }$
So, symbol $\cap$ is called intersection and $A\cap B$ means those elements which belong to both Set A and Set B.
So, $A\cap B=\\{2,4,6,8,10\\}$, as in Set A and Set B, 2, 4, 6, 8, and 10 are only common elements that belong to both Set A and B.
Now in question, it is given that $A\cap B=B$.
We know that if $x\in A\cap B$ then $x\in A$ and $x\in B$.
Now, $A\bigcap B=B$implies that $\forall y\in A\cap B\Rightarrow y\in B$
And $\forall z\in B\Rightarrow z\in A\cap B$.
Now, we try to find the position of a point in set B with respect to set A.
So,
$\begin{aligned} & \forall z\in B \\\ & \Rightarrow z\in A\cap B \\\ & \Rightarrow z\in A \\\ \end{aligned}$
Now, the above line tells us that $B\subseteq A$.

Note: We can also solve the above problem using Venn diagram.
The Venn diagram for $A\cap B=B$ will be

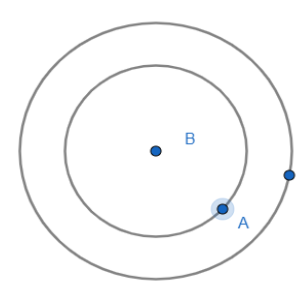
The inner-circle being the set B and the outer circle being the set A.
So, from observation, we can tell that $B\subseteq A$.