Question

Compare the areas under the curves $y={{\cos }^{2}}x\ and\ y={{\sin }^{2}}x$ between $x=0\ and\ x=\pi$.

Answer 1

Hint: We will first start by drawing the rough sketch of the graph of both $y={{\cos }^{2}}x\ and\ y={{\sin }^{2}}x$. Then we will find the area between $x=0\ and\ x=\pi$ and then compare the result.

Complete step-by-step answer:
Now, we will first draw the graph of $y={{\sin }^{2}}x\ and\ y={{\cos }^{2}}x$,


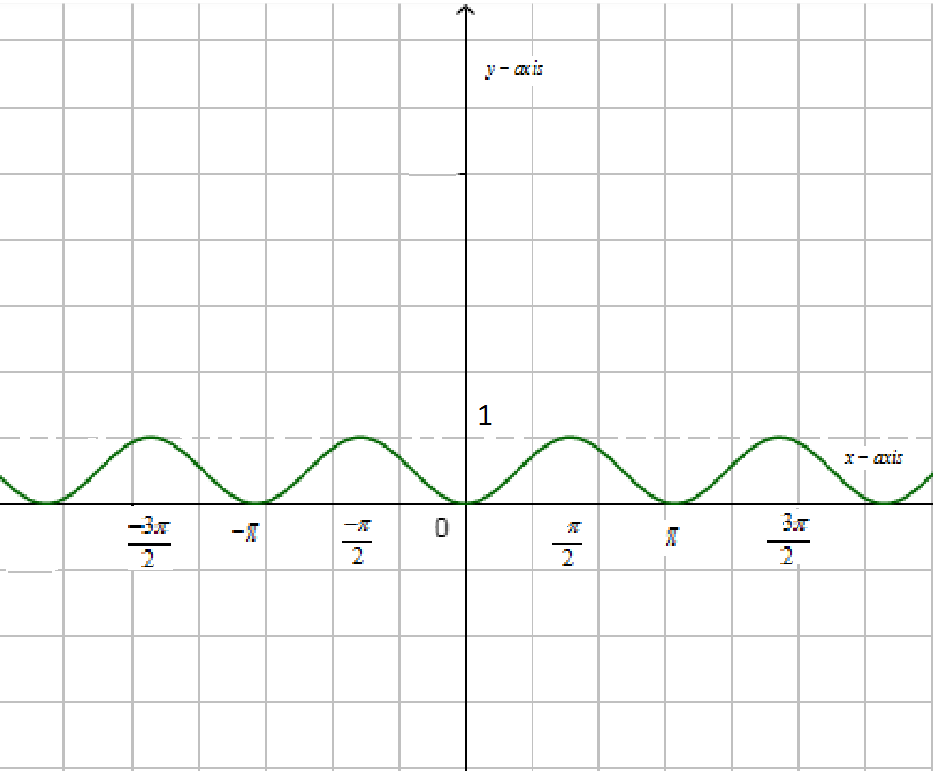
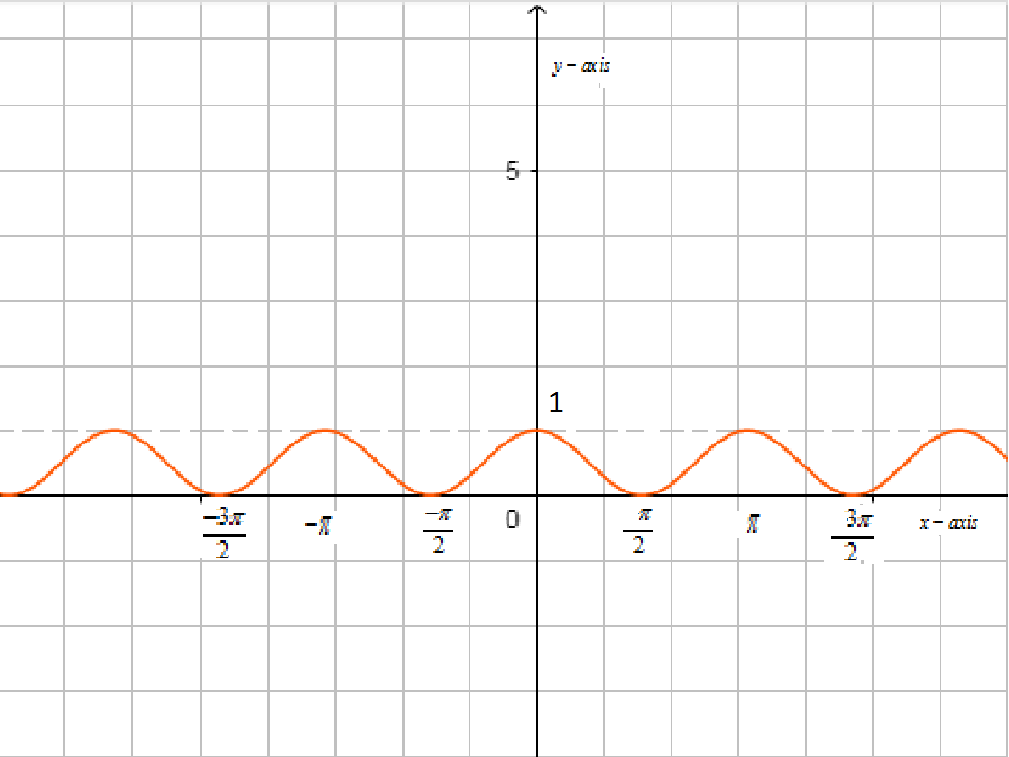
Now, we have to find the area of ${{\sin }^{2}}x$ between $0\ to\ \pi$. We know that the area under the curve is $\int{f\left( x \right)dx}$.
$\Rightarrow \int\limits_{0}^{\pi }{{{\sin }^{2}}xdx}$
Now, we know the trigonometric identity that,
$\begin{aligned} & \cos 2x=1-2{{\sin }^{2}}x \\\ & \Rightarrow 1-\cos 2x=2{{\sin }^{2}}x \\\ & \Rightarrow {{\sin }^{2}}x=\dfrac{1-\cos 2x}{2} \\\ \end{aligned}$
Now, using this in integral we have,

& \int\limits_{0}^{\pi }{\left( \dfrac{1-\cos 2x}{2} \right)} \\\ & \Rightarrow \int\limits_{0}^{\pi }{\left( \dfrac{1}{2}-\dfrac{1}{2}\cos 2x \right)}dx \\\ \end{aligned}$$ Now, we know that, $$\begin{aligned} & \int{\cos 2\theta =\dfrac{\sin 2\theta }{2}} \\\ & \Rightarrow \left( \dfrac{1}{2}x-\dfrac{1}{2}\dfrac{\sin 2x}{2} \right)_{0}^{\pi } \\\ & \Rightarrow \left. \dfrac{x}{2} \right|_{0}^{\pi }-\dfrac{1}{4}\left. \times \sin 2x \right|_{0}^{\pi } \\\ & \Rightarrow \dfrac{\pi }{2}-\dfrac{1}{4}\left( \sin 2\pi -\sin 0 \right) \\\ & \Rightarrow \dfrac{\pi }{2}-\dfrac{1}{4}\left( 0-0 \right) \\\ & \Rightarrow \dfrac{\pi }{2}sq\ units \\\ \end{aligned}$$ Now, similarly for the area of $${{\cos }^{2}}x$$ we have, $$\Rightarrow \int\limits_{0}^{\pi }{{{\cos }^{2}}xdx}$$ Now, we know that $$\begin{aligned} & \cos 2x=2{{\cos }^{2}}x-1 \\\ & \dfrac{\cos 2x+1}{2}={{\cos }^{2}}x \\\ \end{aligned}$$ So, using this we have, $$\begin{aligned} & \int\limits_{0}^{\pi }{\left( \dfrac{\cos 2x+1}{2} \right)}dx \\\ & \Rightarrow \int\limits_{0}^{\pi }{\left( \dfrac{\cos 2x}{2}+\dfrac{1}{2} \right)}dx \\\ & \Rightarrow \left( \dfrac{\sin 2x}{4}+\dfrac{1}{2}x \right)_{0}^{\pi } \\\ & \Rightarrow \dfrac{\sin \left( 2\pi \right)-\sin \left( 0 \right)}{2}+\dfrac{1}{2}\left( \pi -0 \right) \\\ & \Rightarrow \dfrac{0-0}{4}+\dfrac{\pi }{2} \\\ & \Rightarrow \dfrac{\pi }{2}sq\ units \\\ \end{aligned}$$ Now, we can see that the area of both $${{\sin }^{2}}x\ and\ {{\cos }^{2}}x$$ is $$\dfrac{\pi }{2}$$ between $$0\ to\ \pi $$. Hence, their area is the same. Note: It is important to note that we have used the trigonometric identity that $\cos 2x=1-2{{\cos }^{2}}x$ to solve the integral. Also, we have used the trigonometric identity that $\sin 2\pi =0$ and sin 0 = 0 to further solve it.