Question

Compare a step-up transformer with a step- down transformer based on the number of loops in the primary and secondary coil.

Answer 1

Recollect the principle and construction of the transformer along with the number of turns in secondary and primary coil. Later find the difference between the step- up and step-down transformer.

Complete step-by-step answer:
Alternating voltages can be changed into any desired value with the help of a device called a Transformer. It works on the principle of mutual induction. In construction, it consists of a closed laminated iron core of low hysteresis loss. The laminations are insulated from one another to minimize eddy current losses. Two coils are wound over the limbs of the core. One of the coils is called the primary and the other secondary. The primary coil connected to the source of alternating voltage and an output voltage appears across the terminals of the secondary coil due to induction.

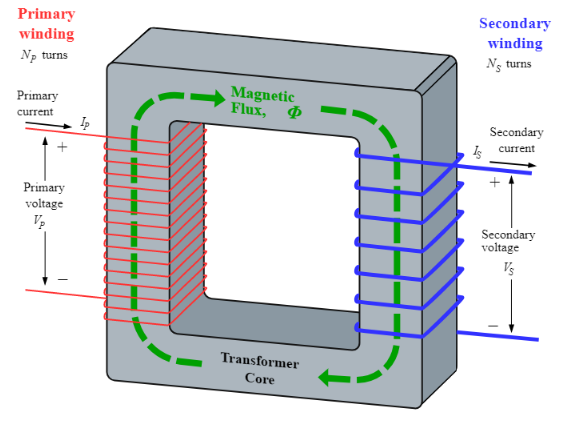
When an alternating voltage is applied to the primary, current flows through it and the core is magnetized. The alternating magnetic flux produced by this current links the secondary coil and induces an emf in it. As a result, an alternating voltage appears across the secondary coil as output voltage. The output voltage across the secondary coil depends on the input voltage across the primary coil and ratio of number of turns in secondary coil to that in the primary coil (also known as turns ratio).
The induced emf in the secondary with ${{\text{N}}_{\text{s}}}$ turns is,
$\Rightarrow {{{\epsilon }}_s} = - {N_s}\dfrac{{d\phi }}{{dt}}$
The alternating magnetic flux $\phi$ also includes a back emf in the primary and it is,
$\Rightarrow {{{\epsilon }}_p} = - {N_p}\dfrac{{d\phi }}{{dt}}$
Where, ${N_p}$ is the number of turns in the primary coil. If ${{\text{V}}_{\text{p}}}$ is the applied voltage across primary and ${V_s}$is the output voltage across secondary, we have ${\varepsilon _p}{\text{ = }}{{\text{V}}_{\text{p}}}{\text{ and }}{\varepsilon _s}{\text{ = }}{{\text{V}}_s}{\text{ }}$
That is,
$\Rightarrow {V_s} = - {N_s}\dfrac{{d\phi }}{{dt}}$ and
$\Rightarrow {V_p} = - {N_p}\dfrac{{d\phi }}{{dt}}$
$\therefore \dfrac{{{V_s}}}{{{V_p}}} = \dfrac{{{N_s}}}{{{N_p}}}$
Thus,
$\Rightarrow \dfrac{{{I_p}}}{{{I_s}}} = \dfrac{{{V_s}}}{{{V_p}}}$
$\therefore \dfrac{{{N_s}}}{{{N_p}}}$
If the secondary coil has a greater number of the turns than primary coil, $\left( {{N_s} > {N_p}} \right)$, the output voltage across secondary is more than the input voltage across primary $\left( {{V_s} > {V_p}} \right)$. This type of transformer is called a step-up transformer. However, in this case, current in the secondary coil is less than current in primary coil $\left( {{I_s} < {I_p}} \right)$ .
If the secondary coil has less turns than the primary coil, $\left( {{N_s} < {N_p}} \right)$, then the output voltage across the secondary is less than input voltage across the primary, $\left( {{V_s} < {V_p}} \right)$ .this type of transformer is called step-down transformer. In this case, current in secondary is more than the current in primary $\left( {{I_s} > {I_p}} \right)$.

Note: In this type of question, remember current and voltage (output and input) are not proportional.
Step up transformer is a transformer in which the low voltage winding is connected to the input or power source and the high voltage winding is connected to the output or load.