Question

Column I	Column II	Column III
(a) NO₂ (i) Sn/HCl (ii) OH⁻	(p) NH₂	(1) n-factor is 1
(b) NO₂ LAH	(q) NO	(2) n-factor is 2
(c) NO₂ Zn NH₄Cl	(r) NHOH	(3) n-factor is 4
(d) NO₂ Fe HCl	(s) N=N-Ph	(4) n-factor is 6

Which of the following combinations is correct?

Answer 1

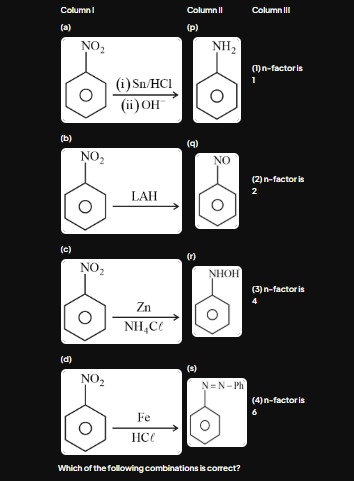
(c)-(r)-(3)

Answer 2

The question asks to identify the correct combination of a reaction, its product, and the corresponding n-factor (change in oxidation state of nitrogen).

Let's analyze each option:

General Information: Oxidation state of Nitrogen in Nitrobenzene In nitrobenzene (C₆H₅NO₂), the phenyl group is neutral. Let the oxidation state of N be x. x + 2(-2) = 0 (Oxygen is -2) x - 4 = 0 x = +4 So, the initial oxidation state of nitrogen in nitrobenzene is +4.

---

Case (a): Nitrobenzene (C₆H₅NO₂) with Sn/HCl (i) then OH⁻ (ii)

• Reaction & Product: Sn/HCl is a strong reducing agent that completely reduces the nitro group (-NO₂) to an amino group (-NH₂). So, C₆H₅NO₂ is reduced to C₆H₅NH₂ (aniline). This matches product (p).
• Oxidation state of N in Aniline (C₆H₅NH₂): Let the oxidation state of N be y. y + 3(1) = 0 (Hydrogen is +1) y + 3 = 0 y = -3
• n-factor: Change in oxidation state of N = |Final oxidation state - Initial oxidation state| n-factor = |(-3) - (+4)| = |-7| = 7.
• Column III (1) states n-factor is 1. This is incorrect. Therefore, the combination (a)-(p)-(1) is incorrect.

---

Case (b): Nitrobenzene (C₆H₅NO₂) with LAH (Lithium Aluminium Hydride)

• Reaction & Product: LAH is a very strong reducing agent. It typically reduces nitrobenzene to azoxybenzene, azobenzene, hydrazobenzene, or even aniline, depending on conditions and stoichiometry. It does not typically stop at nitrosobenzene (C₆H₅NO) as the major stable product. However, for the sake of evaluating the n-factor, let's assume the product is (q) Nitrosobenzene (C₆H₅NO).
• Oxidation state of N in Nitrosobenzene (C₆H₅NO): Let the oxidation state of N be y. y + (-2) = 0 (Oxygen is -2) y = +2
• n-factor: Change in oxidation state of N = |(+2) - (+4)| = |-2| = 2.
• Column III (2) states n-factor is 2. This matches the calculated n-factor if the product is nitrosobenzene. While the reaction to produce nitrosobenzene as a primary product with LAH is not standard, the n-factor calculation matches. We will compare this with other options.

---

Case (c): Nitrobenzene (C₆H₅NO₂) with Zn/NH₄Cl

• Reaction & Product: Reduction of nitrobenzene with Zn/NH₄Cl (in neutral medium) is a standard method to produce N-phenylhydroxylamine. So, C₆H₅NO₂ is reduced to C₆H₅NHOH. This matches product (r).
• Oxidation state of N in Phenylhydroxylamine (C₆H₅NHOH): Let the oxidation state of N be y. y + 1(1) + 1(1) + 1(-2) = 0 (H is +1, O is -2) y + 1 + 1 - 2 = 0 y = 0
• n-factor: Change in oxidation state of N = |(0) - (+4)| = |-4| = 4.
• Column III (3) states n-factor is 4. This matches the calculated n-factor. Therefore, the combination (c)-(r)-(3) is correct, both in terms of reaction and n-factor.

---

Case (d): Nitrobenzene (C₆H₅NO₂) with Fe/HCl

• Reaction & Product: Fe/HCl, like Sn/HCl, is a strong reducing agent in acidic medium. It reduces the nitro group to an amino group, forming aniline (C₆H₅NH₂). The product given in Column II is (s) Azobenzene (C₆H₅N=NC₆H₅). Azobenzene is typically formed by reduction of nitrobenzene in alkaline medium (e.g., Zn/NaOH). So, this reaction is generally incorrect for Fe/HCl.
• Oxidation state of N in Azobenzene (C₆H₅N=NC₆H₅): In azobenzene, each nitrogen atom is bonded to a carbon atom (less electronegative) and another nitrogen atom via a double bond. The N=N bond does not contribute to the oxidation state of individual N atoms as it's between identical atoms. Each N forms one bond with carbon. Since N is more electronegative than C, N gains one electron from the C-N bond. So, the oxidation state of N in azobenzene is -1.
• n-factor (per mole of nitrobenzene): Change in oxidation state of N = |(-1) - (+4)| = |-5| = 5.
• Column III (4) states n-factor is 6. This is incorrect (it should be 5). Therefore, the combination (d)-(s)-(4) is incorrect.

---

Conclusion: Based on the analysis, the only combination that is consistently correct in terms of both the reaction/product and the n-factor is (c)-(r)-(3).