Question
Question: The value of $\bigg|4\bigg(2cos^3\frac{\pi}{7}-cos^2\frac{\pi}{7}-cos\frac{\pi}{7}\bigg)\bigg|$ is...
The value of 4(2cos37π−cos27π−cos7π) is
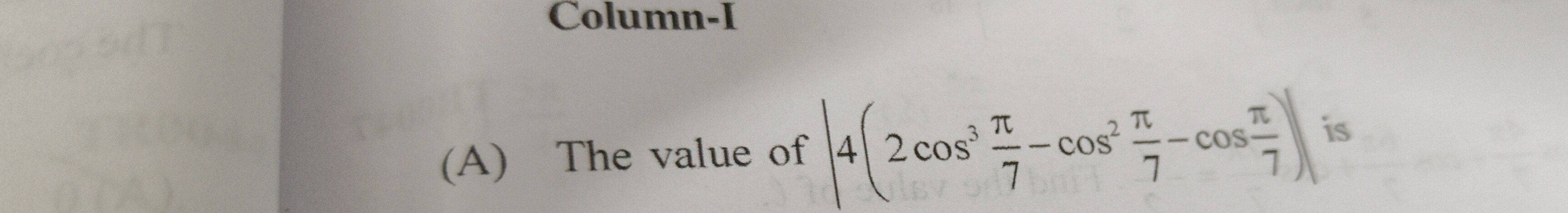
1
Solution
Let x=7π. The expression inside the absolute value is E=4(2cos3x−cos2x−cosx).
We use the triple angle formula for cosine: cos(3x)=4cos3x−3cosx. From this, 4cos3x=cos(3x)+3cosx. Dividing by 2, 2cos3x=21(cos(3x)+3cosx).
Substitute this into the expression for E: E=4(21(cos(3x)+3cosx)−cos2x−cosx) E=2(cos(3x)+3cosx)−4cos2x−4cosx E=2cos(3x)+6cosx−4cos2x−4cosx E=2cos(3x)+2cosx−4cos2x
Next, we use the double angle formula for cosine: cos(2x)=2cos2x−1. From this, 2cos2x=1+cos(2x). So, 4cos2x=2(1+cos(2x))=2+2cos(2x).
Substitute this into the expression for E: E=2cos(3x)+2cosx−(2+2cos(2x)) E=2cos(3x)+2cosx−2−2cos(2x) E=2cos(3x)−2cos(2x)+2cosx−2.
Now, we need to evaluate this expression with x=7π. Consider the roots of the equation z7−1=0. These are zk=ei72kπ for k=0,1,…,6. Since z7−1=(z−1)(z6+z5+z4+z3+z2+z+1), the roots of z6+z5+z4+z3+z2+z+1=0 are zk=ei72kπ for k=1,2,…,6. Divide the equation z6+z5+z4+z3+z2+z+1=0 by z3 (since z=0): z3+z2+z+1+z1+z21+z31=0 Group terms: (z3+z31)+(z2+z21)+(z+z1)+1=0. For z=eiθ, we know zn+zn1=2cos(nθ). Let θ=72π. Then z=ei72π. Substituting into the grouped equation: 2cos(3⋅72π)+2cos(2⋅72π)+2cos(72π)+1=0 2cos(76π)+2cos(74π)+2cos(72π)+1=0.
Now, relate these angles to 7π: cos(76π)=cos(π−7π)=−cos(7π). cos(74π)=cos(π−73π)=−cos(73π).
Substitute these back into the equation: 2(−cos7π)+2(−cos73π)+2cos72π+1=0 −2cos7π−2cos73π+2cos72π+1=0. Rearranging this equation, we get: 2cos72π−2cos73π−2cos7π=−1.
Let's compare this with our expression for E: E=2cos73π−2cos72π+2cos7π−2. Notice that the first three terms of E are the negative of the left side of the equation we derived: −(2cos72π−2cos73π−2cos7π)=−(−1)=1. So, 2cos73π−2cos72π+2cos7π=1.
Substitute this value back into the expression for E: E=1−2=−1.
Finally, we need to find the absolute value: ∣E∣=∣−1∣=1.
