Question

Match the following:

Column- I	Column-II
(A) $x^{\frac{3}{4}(log_3 x)^2 + log_3 x - \frac{5}{4}} = \sqrt{3}$	(p) number of solutions = 2
(q) number of solutions = 3
(r) number of solution = 1
(s) number of solution = 0
(t) infinite number of solutions
(B) $log_{0.2} \frac{x+2}{x} \leq 1$
(C) $log_2 (x+5) = 6-x$

Answer 1

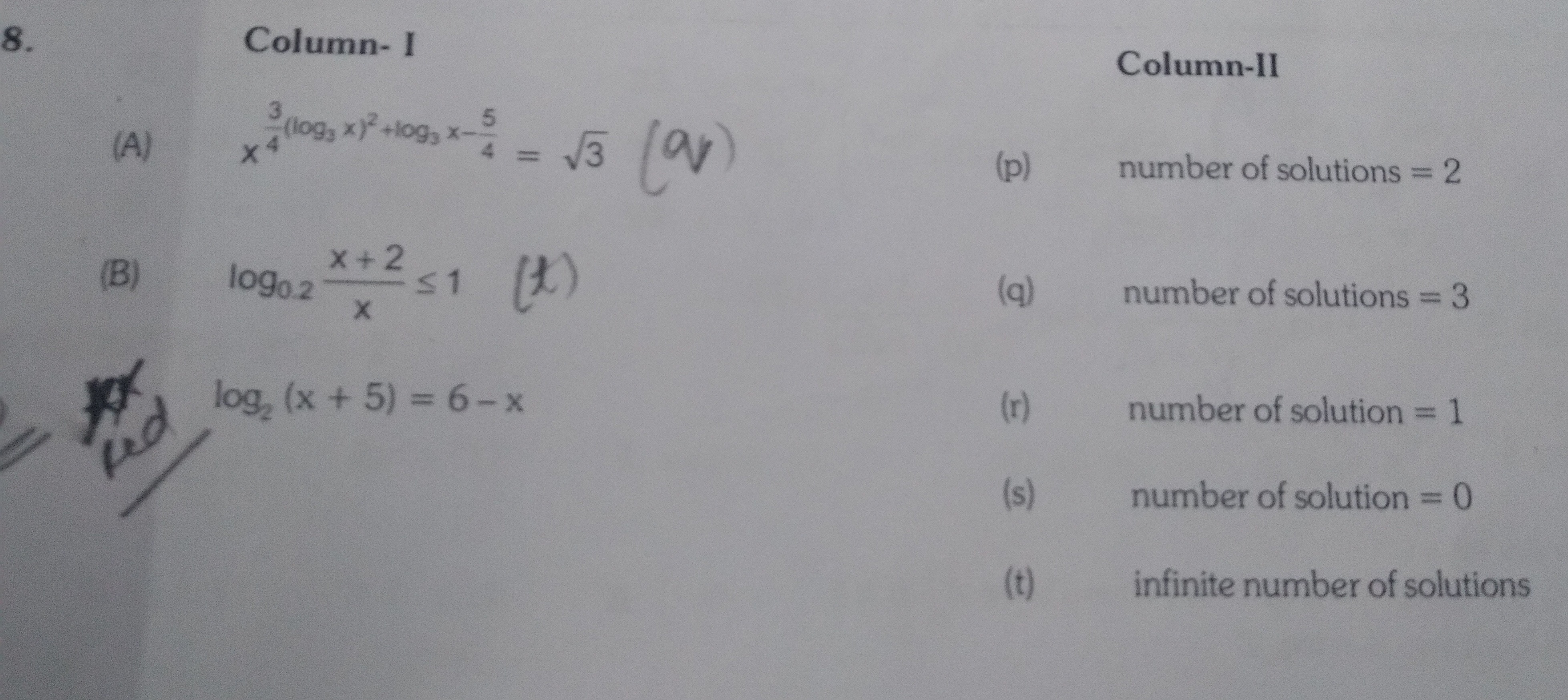
(A)-(q), (B)-(t), (C)-(r)

Answer 2

(A) Let $y = \log_3 x$. The equation becomes $x^{\frac{3}{4}y^2 + y - \frac{5}{4}} = 3^{1/2}$. Taking $\log_3$ on both sides: $(\frac{3}{4}y^2 + y - \frac{5}{4}) \log_3 x = \frac{1}{2} \log_3 3$ $(\frac{3}{4}y^2 + y - \frac{5}{4}) y = \frac{1}{2}$ $\frac{3}{4}y^3 + y^2 - \frac{5}{4}y = \frac{1}{2}$ Multiply by 4: $3y^3 + 4y^2 - 5y = 2$ $3y^3 + 4y^2 - 5y - 2 = 0$ We can see that $y=1$ is a root: $3(1)^3 + 4(1)^2 - 5(1) - 2 = 3+4-5-2 = 0$. So $(y-1)$ is a factor. Performing polynomial division or synthetic division: $(y-1)(3y^2 + 7y + 2) = 0$ $(y-1)(3y+1)(y+2) = 0$ The roots are $y=1$, $y = -1/3$, $y = -2$. Since $y = \log_3 x$, we have: $\log_3 x = 1 \implies x = 3^1 = 3$ $\log_3 x = -1/3 \implies x = 3^{-1/3}$ $\log_3 x = -2 \implies x = 3^{-2}$ All three values of $x$ are valid. Thus, there are 3 solutions. (q)

(B) The domain requires $\frac{x+2}{x} > 0$, which means $x \in (-\infty, -2) \cup (0, \infty)$. The inequality is $log_{0.2} \frac{x+2}{x} \leq 1$. Since the base $0.2 < 1$, the inequality reverses when we remove the logarithm: $\frac{x+2}{x} \geq (0.2)^1 = \frac{1}{5}$ $\frac{x+2}{x} - \frac{1}{5} \geq 0$ $\frac{5(x+2) - x}{5x} \geq 0$ $\frac{5x+10-x}{5x} \geq 0$ $\frac{4x+10}{5x} \geq 0$ $\frac{2(2x+5)}{5x} \geq 0$ The critical points are $x = -5/2$ and $x = 0$. The inequality holds for $x \in (-\infty, -5/2] \cup (0, \infty)$. Intersecting this with the domain $x \in (-\infty, -2) \cup (0, \infty)$: The intersection is $(-\infty, -5/2] \cup (0, \infty)$. This set contains an infinite number of solutions. (t)

(C) The domain requires $x+5 > 0$, so $x > -5$. Consider the functions $f(x) = \log_2 (x+5)$ and $g(x) = 6-x$. $f(x)$ is strictly increasing for $x > -5$. $g(x)$ is strictly decreasing for all $x$. A strictly increasing function and a strictly decreasing function can intersect at most at one point. Let's test some integer values: If $x=3$, $f(3) = \log_2 (3+5) = \log_2 8 = 3$. $g(3) = 6-3 = 3$. So $x=3$ is a solution. Since there can be at most one solution, $x=3$ is the unique solution. Thus, there is 1 solution. (r)

The correct matches are (A)-(q), (B)-(t), (C)-(r).