Question

Circles with radii 3, 4, and 5 touch each other externally if P is the point of intersection of tangents to these circles at their points of contact. Find the distance of P from the points of contact.

Answer 1

Hint: To solve this question, we should have knowledge of incentre. Incentre is nothing but the point inside the triangle such that the circle of that point as center touches all the sides as a tangent. The radius of that circle is the ratio of the area of the triangle to the half of the perimeter of that triangle,
$r=\dfrac{\Delta }{s}$

Complete step-by-step answer:
In this question, we have to find the distance of point P from the points of contact of the circles of radii 3, 4, and 5.

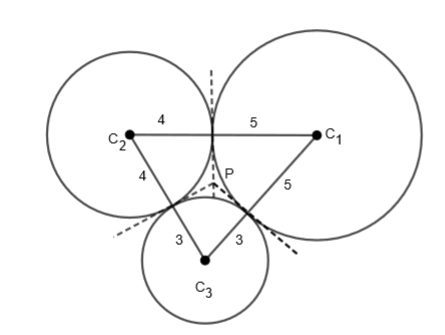
We have constructed this diagram because in the question, we have been given that the circle of radii 3, 4, and 5 touches each other externally and P is the point of intersection of the tangent. As we know that P is the incentre of triangle ${{C}_{1}}{{C}_{2}}{{C}_{3}}$, so we can say that the distance from P to point of the contacts will be the inradius of triangle ${{C}_{1}}{{C}_{2}}{{C}_{3}}$.
Now, we know that the inradius is the ratio of the area of the triangle to the half of the perimeter. So, we can write $r=\dfrac{\Delta }{s}$ where r is the inradius and $\Delta$ is the area and s is half of the perimeter. So, we can write
$s=\dfrac{{{C}_{1}}{{C}_{2}}+{{C}_{2}}{{C}_{3}}+{{C}_{3}}{{C}_{1}}}{2}$
$s=\dfrac{9+7+8}{2}$
$s=\dfrac{24}{2}$
$s=12$
We also know that the area of the triangle $\Delta$ can be calculated by $\sqrt{s\left( s-a \right)\left( s-b \right)\left( s-c \right)}$ from heron’s formula. So, we can write,
$\Delta =\sqrt{12\left( 12-7 \right)\left( 12-8 \right)\left( 12-9 \right)}$
$\Delta =\sqrt{12\left( 5 \right)\left( 4 \right)\left( 3 \right)}$
$\Delta =12\sqrt{5}$
Now, we will put the value of $\Delta$ and s in the formula,
$r=\dfrac{\Delta }{s}$
So, we will get,
$r=\dfrac{12\sqrt{5}}{12}$
$r=\sqrt{5}$
Hence, we can say that the distance from point P to point of contact is $\sqrt{5}$ units.

Note: In this question, we need to remember the formula of inradius in terms of the area of the triangle and perimeter. Also, we should know that the area of the triangle can be calculated using heron's formula, that is, area $=\sqrt{s\left( s-a \right)\left( s-b \right)\left( s-c \right)}$ where $s=\dfrac{a+b+c}{2}$ and a, b and c are the sides of the triangle.