Question

Circle has the equation ${{x}^{2}}+{{y}^{2}}+2x-2y-14=0$. How do you graph the circle using the center $\left( h,k \right)$ and radius,$r$?

Answer 1

Generally the equation of a circle comes in two forms:
1. The standard form:${{\left( x-h \right)}^{2}}+{{\left( y-k \right)}^{2}}={{r}^{2}}$
2. The general form:${{x}^{2}}+{{y}^{2}}+dx+sy+f=0,$ where d, s, f are constants.
If the equation of a circle is in the standard form, we can easily identify the center of the circle,$\left( h,k \right)$, and radius,$r$. But if we have an equation in general form then we have to simplify it by using a few steps.

Complete step by step solution:
Here we have the equation in general form${{x}^{2}}+{{y}^{2}}+2x-2y-14=0$ . To draw the circle we have to find the center, $\left( h,k \right)$and radius, $r$. For we will simplify our given equation${{x}^{2}}+{{y}^{2}}+2x-2y-14=0$ by these steps:
1. Write the equation in this form: $\left( {{x}^{2}}+2x+{{?}_{1}} \right)+\left( {{y}^{2}}-2y+{{?}_{2}} \right)=14+{{?}_{1}}+{{?}_{2}}$ . In the first parenthesis, we group the $x$-terms and in the second the$y$-terms. The constant is moved on the right hand side. Here we have to apply, on both sides of the equation.
2. Now take the coefficient of $x$ and divide it by$2$, $\left( \dfrac{2}{2} \right)$ , and then square it, we get ${{\left( \dfrac{2}{2} \right)}^{2}}=1$ and replace the ${{?}_{1}}$ by $1$.
3. Take coefficient of $y$ and divide it by$2$,$\left( -\dfrac{2}{2} \right)$, and the square it, we get${{\left( -\dfrac{2}{2} \right)}^{2}}=1$ and replace the ${{?}_{2}}$ by$1$.
Putting steps 1-3 together we have the following:
$\begin{aligned} & \Rightarrow \left( {{x}^{2}}+2x+{{?}_{1}} \right)+\left( {{y}^{2}}-2y+{{?}_{2}} \right)=14+{{?}_{1}}+{{?}_{2}} \\\ & \Rightarrow \left( {{x}^{2}}+2x+1 \right)+\left( {{y}^{2}}-2y+1 \right)=14+1+1 \\\ & \Rightarrow {{\left( x+1 \right)}^{2}}+{{\left( y-1 \right)}^{2}}={{4}^{2}} \\\ \end{aligned}$
Now the equation becomes in standard form. The center, $\left( h,k \right)$are -1, 1 and radius, $r$is 4.
The graph of the circle is:

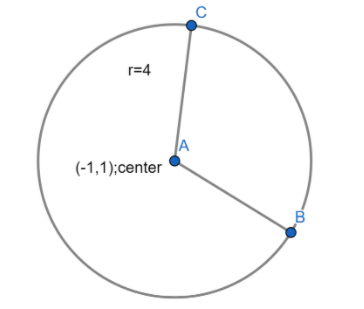
Note:
A common mistake we sometimes made is to take $h=1$, and $k=-1$. In equation, if the sign preceding $h$, and $k$ , $\left( h,k \right)$are negative, then $h$ and $k$ are positive. That is,$h=-1$, and $k=1$ . Always change the general form of the equation into standard form.