Question

Choose the correct option $\sin \left( A+B \right)\cdot \sin \left( A-B \right)$ $$$$
A.{{\sin }^{2}}A-{{\cos }^{2}}B$$$$$ B. {{\cos }^{2}}A-{{\cos }^{2}}B C. ${{\sin }^{2}}A-{{\sin }^{2}}B
D. ${{\sin }^{2}}A-{{\cos }^{2}}B$$$$$

Answer 1

We expand the given trigonometric expression using the angle sum and angle difference formula of sine as $\sin \left( A+B \right)=\sin A\cos B+\cos A\sin B$ and $\sin \left( A-B \right)=\sin A\cos B-\cos A\sin B$ respectively, use algebraic identity $\left( a+b \right)\left( a-b \right)={{a}^{2}}-{{b}^{2}}$ and finally use the Pythagorean identity ${{\cos }^{2}}\theta =1-{{\sin }^{2}}\theta$ to find the required expression.$$$$

Complete step-by-step answer:

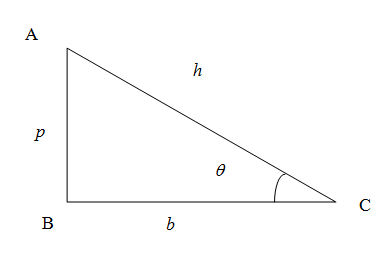
We know that in right angled triangle the side opposite to right angled triangle is called hypotenuse denoted as $h$, the vertical side is called perpendicular denoted as $p$ and the horizontal side is called the base denoted as $b$.$$$$

We know from the trigonometric ratios in a right angled triangle the sine of any angle is given by the ratio of side opposite to the angle to the hypotenuse. In the figure the sine of the angle $\theta$ is given by
$\sin \theta =\dfrac{p}{h}$
Similarly the cosine of an angle is the ratio of side adjacent to the angle (excluding hypotenuse) to the hypotenuse. So we have cosine of angle
$\cos \theta =\dfrac{b}{h}$
We know from compound angle formula or angle sum formula of sine that if there are two angles say $A,B$ then the sum of sine of their sum is given in terms of sine and cosine of $A,B$ as
$\sin \left( A+B \right)=\sin A\cos B+\cos A\sin B$
We know from angle difference formula of sine that is
$\sin \left( A-B \right)=\sin A\cos B-\cos A\sin B$
We know from Pythagorean trigonometric identities that for some angle $\theta$ that the sine and cosine of same angle $\theta$ are related as

& {{\sin }^{2}}\theta +{{\cos }^{2}}\theta =1 \\\ & \Rightarrow {{\cos }^{2}}\theta =1-{{\sin }^{2}}\theta \\\ \end{aligned}$$ We are given in the question the equation $$\sin \left( A+B \right)\cdot \sin \left( A-B \right)$$ We use angle sum and angle difference formula of sine and proceed to have $$=\left( \sin A\cos B+\cos A\sin B \right)\left( \sin A\cos B-\cos A\sin B \right)$$ We use the algebraic identify $\left( a+b \right)\left( a-b \right)={{a}^{2}}-{{b}^{2}}$ in the above step for $a=\sin A\cos B+\cos A\sin B,b=\sin A\cos B-\cos A\sin B$ to have, $$\begin{aligned} & ={{\left( \sin A\cos B \right)}^{2}}-{{\left( \cos A\sin B \right)}^{2}} \\\ & ={{\sin }^{2}}A{{\cos }^{2}}B-{{\cos }^{2}}A{{\sin }^{2}}B \\\ \end{aligned}$$ We Pythagorean trigonometric identity of sine-cosine to convert sine to cosine for $\theta =B,A$ as, $$\begin{aligned} & ={{\sin }^{2}}A\left( 1-{{\sin }^{2}}B \right)-\left( 1-{{\sin }^{2}}A \right){{\sin }^{2}}B \\\ & ={{\sin }^{2}}A-{{\sin }^{2}}A{{\sin }^{2}}B-{{\sin }^{2}}B + {{\sin }^{2}}A{{\sin }^{2}}B \\\ & ={{\sin }^{2}}A-{{\sin }^{2}}B \\\ \end{aligned}$$ **So, the correct answer is “Option A”.** **Note:** We can further put ${{\sin }^{2}}\theta =1-{{\cos }^{2}}\theta ,\theta =A,B$ to obtain the result in cosines ${{\cos }^{2}}B-{{\cos }^{2}}A$. We must be careful of the confusion between the angle sum and angle difference formula of sine from cosine which has the formulae $\cos \left( A+B \right)=\cos A\cos B-\sin A\sin B$ and $\cos \left( A-B \right)=\cos A\cos B+\sin A\sin B$. We can use these formulae to similarly get $\cos \left( A+B \right)\cos \left( A-B \right)={{\cos }^{2}}A-{{\sin }^{2}}B={{\sin }^{2}}A-{{\cos }^{2}}B$